Physics
Combining Waves
Combining wave functions to compare or contrast them.
Damped Motion
A model that describes a phenomenon maintaining a sinusoidal component, but the amplitude of the component decreases with time to account for the damping effect.
Simple Harmonic Motion
A special kind of vibrational motion in which the acceleration of an object is directly proportional to the negative of its displacement from its rest position.
Area of a Triangle
Area of a triangle.
Example problems
Car Wheel Alignment
Trigonometric equations are used to relight car wheel alignments so the car drives straight. Or for NASCAR, at a slight left angle.
Aviation Flight Computers
Flight Computers use right-angle trigonometry to calculate the approach angle for takeoff and landing.
Car suspension
Car steering
Car engine perfomance
The graphs for engine performance such as horsepower, heat, torque, and other factors and be converted into trig functions.
SAA, ASA,SSA,AAA,SAS,SSS
How to solve triangles using only 3 pieces of given information.
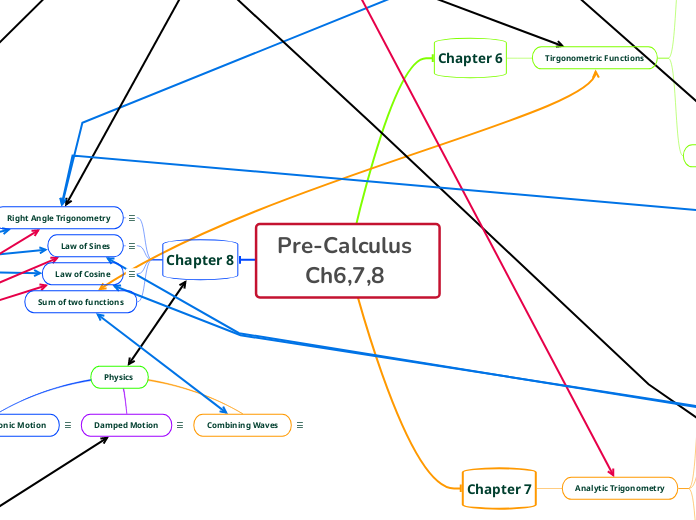
Pre-Calculus Ch6,7,8
Chapter 8
Sum of two functions
Law of Cosine
Law of cosines signifies the relation between the lengths of sides of a triangle with respect to the cosine of its angle.
Law of Sines
The Law of Sines is the relationship between the sides and angles of non-right (oblique) triangles. Simply, it states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all sides and angles in a given triangle.
Right Angle Trigonometry
The basic trig functions can be defined with ratios created by dividing the lengths of the sides of a right triangle in a specific order.
Chapter 7
Analytic Trigonometry
Trigonometric Formulas
Sum and Difference of Sin, Cos, Tan
The sum and difference formulas in trigonometry are used to find the value of the trigonometric functions at specific angles where it is easier to express the angle as the sum or difference of unique angles.
Sum-Product
The process of converting sums into products can make a difference between an easy solution to a problem and no solution at all. Two sets of identities can be derived from the sum and difference identities that help in this conversion
Product-Sum
The process of converting products into sums can make a difference between an easy solution to a problem and no solution at all. Two sets of identities can be derived from the sum and difference identities that help in this conversion
Half-Angle
A half-angle trig identity is found by using the basic trig ratios to derive the sum and difference formulas, then utilizing the sum formula to produce the double angle formulas. Finally, manipulating the double angle formula reveals the half-angle formulas.
Double-Angle
The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself.
Trigonometric Equations
Identities
Identities hey are expressions that restate the same expression in a different way. In other words, the identities allow you to restate a trig expression in a different format, but one which has the exact same value.
Even-Odd
An even function is a function where the value of the function acting on an argument is the same as the value of the function when acting on the negative of the argument
In contrast, an odd function is a function where the negative of the function's answer is the same as the function acting on the negative argument
Pythagorean
Pythagorean identities are identities in trig that are extensions of the Pythagorean theorem. The fundamental identity states that for any angle.
Reciprocal
eciprocal identities are the reciprocals of the three main trig functions sine, cosine, and tangent.
Quotient
Quotient identities are trigonometric identities that are written as fractions of the sine and cosine functions. The tangent forms a quotient identity and can be written as the sine of the angle divided by the cosine. Similarly, the cotangent can be written as the cosine of the angle divided by the sine.
Inverse of Sin, Cos, Tan
Chapter 6
Tirgonometric Functions
The 6 Trigonometric Functions
Sinusoidal Functions
Phase Shift
The phase shift is how far the function is shifted horizontally either to the right or left.
Period
The period of a function refers to the distance of a function's wave.
Amplitude
The amplitude of a trigonometric function is half the distance from the highest point of the curve to the bottom point of the curve.
Unit Circle Approach
A unit circle is a circle of unit radius with center at origin. A circle is a closed geometric figure such that all the points on its boundary are at equal distance from its center. For a unit circle, this distance is 1 unit, or the radius is 1 unit.
Radian Form
Angles in radian form which is written as pi in a faction or whole number
Area of a sector
Area of a circle
conversion from radians to degrees
Radians
Arc of a circle
Angles and their measure
Angles in degree form
Decimal and Degree, minute, second form
Vertex
Initial side
Terminal Side
Right Angle
360 degrees