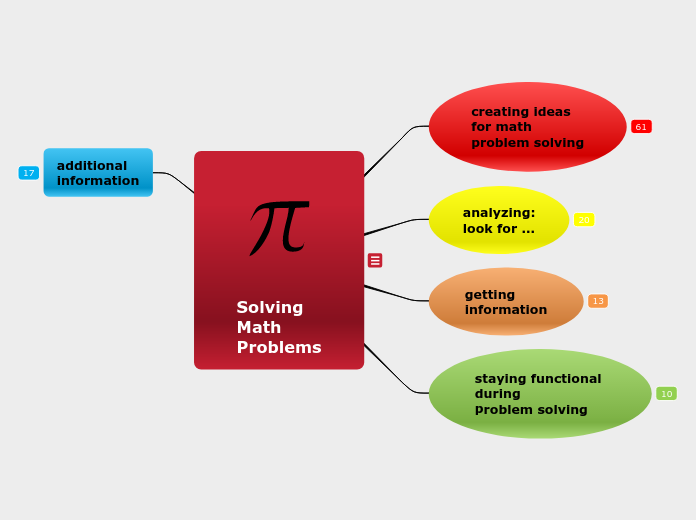
Solving
Math
Problems
This map contains a number of ideas on solving math problems.
The map deals with general problem solving tools that are not specific for one area, e.g. you will find nothing specific on dealing with polynomes or inequalities.
Most of the ideas are taken from the following sources:
Engel, Arthur: Problem Solving Strategies
Polya, George: How To Solve It
Zeitz, Paul: The Art and Craft of Problem Solving
additional
information
Math Problem Solving: Links
Art of Problem Solving
several articles on scribd.com
Mind Mapping and Math Problem Solving
Mathematical Problem Solving and Mind Mapping
Mathematical Problem Solving Strategies
Tips on Problem Solving
MATHCOUNTS article on Problem-Solving strategies
Heuristixx: Math Problem Solving and Mind Mapping
Fifty Problem Solving Strategies Explained
Problem Solving area of the nzmaths website.
Changes tothis map
new "SCREAM" tool added
How to use this map
Here are a number of ideas how you can use this map.
modify this map
There are a number of ways to modify this map.
a) Modify t h i s map.
b) Modify a copy of this map. With a view to collective knowledge, a) seems preferable.
However, mindomo has not (yet) version management functions, so all previous versions of this map are lost.
If you modify this map - could you please leave a note at the "Log and Comments" branch?
print this map
Here are some ideas on printing:
If you are logged in as a mindomo user, you have a number of export functions:
- export to pdf
- export to image file: png, jpg
- export to text: rtf, txt
If you want to print the map as an image, choose the branches you are interested in and hide the rest.
The map is large, so use the largest paper size you can manage.
You can use the print as a problem solving poster.
read this map
staying functional
during
problem solving
persist
breathe deeply and calmly
remember previous successes
exercise
eat / drink something
work in a new setting
take a break
sleep over it
talk to someone
getting
information
use the internet
use math databases
use newsgroups
use forums
email people
use literature
journals
books
math reviews
ask people
experts
fellow students
teachers
analyzing:
look for ...
SPLENDID
To memorize common methods of analyzing math problems, we use the keyword SPLENDID - it stands for
S: look for SYMMETRIES
P: look for PATTERNS
L: look at LIMITS
E: look at EXTREME cases
N: is a rather useful letter in this keyword;-)
D: collect DATA
I: look for INVARIANTS
D: take a more / less DETAILED look
details - take a more / less detailed look
I
invariants - look for invariants
D
data - collect data
organize data
in mind maps
in trees
in tables
N
extremes - look at extreme cases
L
limits - look at limits
P
patterns - look for patterns
symmetry - look for symmetries
creating ideas
for math
problem solving
basic concept: combine OBJECTS and ACTIONS
Combining OBJECTS and ACTIONS is basically a math creativity technique:
It leads to a large number of seminal ideas to tackle a (math) problem.
The underlying ideas are of course not restricted to m a t h problem solving.
ACTIONS
To make the actions easier to memorize, we use the keyword "SCREAM".
It will be clear in a moment how this is meant - look at the next branches.
You may have guessed that I'm not a native speaker of English. So if someone comes up with better keywords - help is greatly appreciated.
manipulate
To remember some of the most important mathematical manipulation actions, we use the keyword SCREAM - it stands for
S: substitute
C: combine; create
R: rearrange; reverse
E: eliminate
A: adapt
M: modify; magnify, minimize
(This is largely inspired by Michael Michalkos "SCAMPER" creativity technique.)
SCREAM
M
minimize
magnify
modify
A
add
adapt
E
exchange
eliminate
R
reverse
rearrange
C
create
combine
S
substitute
OBJECTS
search direction
backward
forward
math objects
relations
inequalities
equations
matrices
sets
numbers
functions
general math tools
series
graphs
complex numbers
representions of the problem
Finding an appropriate representation of a problem is often crucial for finding a solution.
Example: A problem may be very ugly in cartesian coordinates, but can be treated nicely in polar coordinates.
algorithms
geometry
coordinate systems
algebra
number representations
......
binary
number systems
proof techniques
These proof techniques are standard. More information can be found in
Arthur Engel: Problem Solving Strategies
Paul Zeitz: The Art and Craft of Problem Solving
using symmetry
pigeonhole principle
using extremal cases
using invariance
by induction
by contradiction
by direct proof
problem elements
From a v e r y abstract point of view, a problem consists of
- the unknown
- the data and
- the condition.
This idea is taken from George Polya's "How to Solve It".
What is the condition?
What are the data?
What is the unknown?