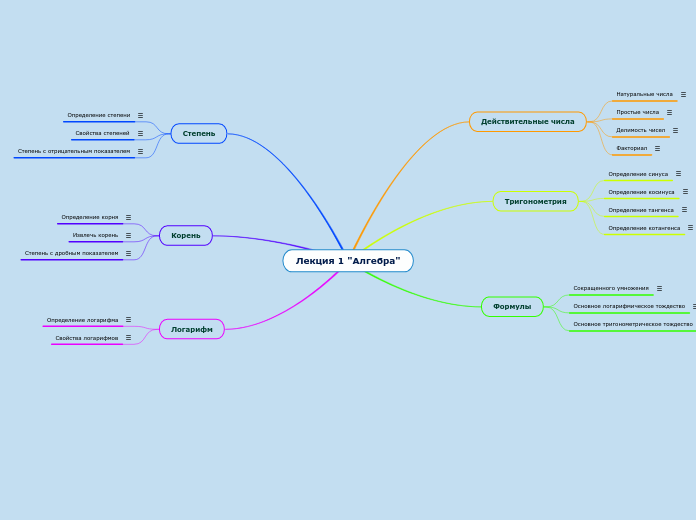
Лекция 1 "Алгебра"
Действительные числа
Натуральные числа
Натуральные числа - это числа, которые используются при счете 1, 2, 3,... .
Простые числа
Простые числа имеют два делителя: 1 и само число.Например, 17=1*17 , т.е. 17 - это простое число;18=1*2*3*3 , т.е. 18 не является простым числом, его называют составным.
Делимость чисел
Делители числа 65526552=2*2*2*3*3*7*13
Факториал
Факториал - это произведение натуральных чисел от 1 до n.Например, 5!=1*2*3*4*5
Тригонометрия
Определение синуса
Число, равное ординате точки единичной окружности, соответствующей углу a, называют синусом угла a и обозначают sin a.
Определение косинуса
Число, равное абсциссе точки единичной окружности, соответствующей углу a, называют косинусом угла a и обозначают cos a.
Определение тангенса
Число, равное отношению ординаты точки единичной окружности к ее абсциссе, соответствующей углу a, называют тангенсом угла a и обозначают tg a.
Определение котангенса
Число, равное отношению абсциссы точки единичной окружности к ее ординате, соответствующей углу a, называют котангенсом угла a и обозначают ctg a.
Формулы
Сокращенного умножения
Формулы сокращенного умножения(x+y)^2=x^2+2xy+y^2 (x+y)^3=x^3+3x^2y+3xy^2+y^3
Основное логарифмическое тождество
Основное логарифмическое тождествоlog(a, a^b)=b
Основное тригонометрическое тождество
Основное тригонометрическое тождество(sin a)^2+(cos a)^2=1
Степень
Определение степени
Под степенью понимают произведение одинаковых множителей, каждым из которых является число a.a^n=a*a*...*a , число a повторяется n раз.
Свойства степеней
Свойства степеней:При умножении степеней с одинаковыми основаниями, основание сохраняется, о показатели складываются.При делении степеней с одинаковыми основаниями, основание сохраняется, а показатели вычитаются.При возведении степень в степень показатели перемножаются.При умножении степеней с одинаковыми показателями, можно перемножить их основания, а показатель сохранить.При делении степеней с одинаковыми показателями, можно разделить их основания, а показатель сохранить.
Степень с отрицательным показателем
Степень с отрицательным показателем:при возведении числа в отрицательную степень можно заменить основание на обратное число и возвести данное число в положительную степень.
Корень
Определение корня
Корнем степени n из числа b называют такое число a (если оно существует), n -я степень которого равна b.sqrt(3, 125)=5
Извлечь корень
Извлечь корень:При извлечении корня можно заменить подкоренное выражение на простые множители и те множители которые имеют степень корня заменить на основания.
Степень с дробным показателем
Свойства корней:Существует, и притом единственный, корень нечётной степени из любого действительного числа b, при этом корень нечётной степени: а) из положительного числа есть число положительное; б) из отрицательного числа есть число отрицательное; в) из нуля есть нуль.Существует два и только два корня чётной степени из любого положительного числа, которые отличаются только знаками. а) Корень чётной степени из нуля единственный и равен нулю. б) Корня чётной степени из отрицательного числа не существует.Неотрицательный корень степени n из неотрицательного числа b называют арифметическим корнем степени n из числа b.
Логарифм
Определение логарифма
Логарифмом положительного числа b по основанию aa>0 и a не равно 1, называют число A, такое что b=a^A Обозначают так: A=log(a,b) , где a -основание логарифма,b - логарифмическое выражение.
Свойства логарифмов
Свойства логарифмов:Логарифм произведения положительных чисел равен сумме логарифмов этих чисел.Логарифм частного положительных чисел равен разности логарифмов делимого и делителя.Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа.