Звичайні дроби
Звичайний дріб або простий дріб — запис раціонального числа в вигляді відношення двох чисел mn. Ділене m називається чисельником дробу, а дільник n — знаменником дробу.
a
Типи звичайних дробів
1. Правильні дроби: Це дроби, у яких чисельник менший за знаменник і їх значення лежить між 0 і 1. Наприклад, 1/2, 3/4.2. Неправильні дроби: Це дроби, у яких чисельник більший за знаменник. Наприклад, 5/4, 7/3.3. Мішані дроби: Це комбінація цілої частини та дробової частини. Наприклад, 1 1/2, 2 3/4.

Операції зі звичайними дробами
Операції зі звичайними дробами включають додавання, віднімання, множення та ділення. Ось як вони виконуються:1. Додавання: Щоб додати дві звичайні дроби, спочатку переконайтеся, що знаменники в них однакові. Якщо знаменники різні, спочатку знайдіть спільний знаменник, а потім додайте чисельники. Знаменник залишається незмінним. Наприклад: 1/4 + 3/4 = 4/4 = 1.2. Віднімання: Для віднімання двох звичайних дробів так само переконайтеся, що знаменники однакові. Якщо знаменники різні, знайдіть спільний знаменник, а потім відніміть чисельники. Знаменник залишається незмінним. Наприклад: 3/4 - 1/4 = 2/4 = 1/2.3. Множення: Щоб помножити дві звичайні дроби, перемножте чисельники разом і знаменники разом. Наприклад: (2/3) * (4/5) = 8/15.4. Ділення: Щоб поділити одну звичайну дріб на іншу, помножте перший дріб на обернений другого дробу. Обернений дріб отримується шляхом обміну чисельника та знаменника. Наприклад: (2/3) / (4/5) = (2/3) * (5/4) = 10/12 = 5/6.
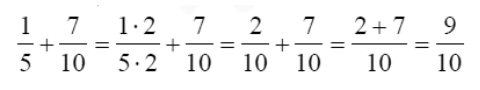
Додавання та віднімання дробів
Додавання (віднімання) дробів: для додавання (віднімання) дробів спочатку необхідно звести їх до загального знаменника, а потім додати (або відняти) чисельники, а знаменник залишиться загальний.
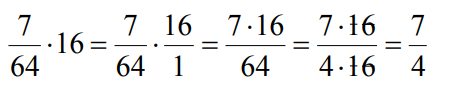
Множення дробів
Множення дробів: для того, щоб помножити один дріб на інший, необхідно помножити чисельник першого дробу на чисельник другого дробу, а знаменник першого дробу на знаменник другого дробу (і, якщо необхідно, ще виконати скорочення загальних множників).

Ділення дробів
Ділення дробів: для того щоб розділити один дріб на інший, необхідно другий дріб перевернути і замінити ділення множення.

Історія виникнення звичайних дробів
Звичайні дроби виникли задовго до писемної історії і є одними з найстаріших математичних концепцій. Вони були розвинуті людством для вирішення практичних проблем, пов'язаних з вимірюванням та поділом об'єктів.Перші згадки про використання дробей можна знайти в стародавніх цивілізаціях Месопотамії (сучасна територія Іраку) і Давньому Єгипті близько 4000 років тому. В Єгипті використовувалися прості дроби для вимірювання земельних ділянок, обчислення об'єму та розрахунків у будівництві.Вавилонські математики, що жили близько 3000 років тому, використовували систему числення, яка базувалася на числі 60 (сексагесимальна система). Вони використовували звичайні дроби для обчислення часу, вимірювання кутів та розрахунків у торгівлі.Давні греки, зокрема великі математики, такі як Піфагор, Евклід та Архімед, вивчали властивості та використання звичайних дробів. Вони використовували дроби для обчислення пропорцій, вимірювання геометричних фігур та розрахунків у науці та інженерії.З часом звичайні дроби стали невід'ємною частиною математики та наукових розрахунків. Вони були розроблені й удосконалені у різних культурах і цивілізаціях, зокрема в Китаї, Індії, Арабському світі та середньовічній Європі.Історія виникнення звичайних дробів є довгим та складним процесом, який розвивався протягом тисячоліть. Сучасна математика використовує звичайні дроби як основні поняття для вирішення різних математичних задач та застосування в різних галузях науки і технологій.
Звичайні дроби у Стародавньому Світі
Звичайні дроби використовувалися в стародавньому світі, особливо в розвинутих цивілізаціях, таких як давній Єгипет, Вавилон, Греція та Рим. Вони використовували дроби для вимірювання кількостей, обчислення площі, об'єму та ваги, а також для розрахунків у торгівлі та інженерних розрахунках.У давньому Єгипті звичайні дроби були широко використовувані для вимірювання площі земельних ділянок та розрахунків у будівництві пірамід. Єгиптяни використовували систему дробів, де чисельник позначався символом лотосового квіту, а знаменник - символом горщика.У Вавилоні використовувалася сексагесимальна система числення, що базувалася на числі 60. Вони використовували звичайні дроби для обчислення часу, вимірювання кутів та розрахунків у торгівлі.Давні греки та римляни також використовували звичайні дроби у своїх розрахунках. Греки використовували дроби для обчислення пропорцій та геометричних фігур. Римляни використовували десяткову систему числення, але також використовували звичайні дроби для обчислення валютних розрахунків та вимірювання об'єму.Звичайні дроби в стародавньому світі були важливим інструментом математики та практичних розрахунків. Вони допомагали людям виконувати складні розрахунки та вимірювання, що були необхідні для розвитку цивілізацій того часу.
Звичайні дроби у Вавилоні
Вперше дроби почали використовувати на території Єгипту і Вавилона. Підхід математиків двох держав мав значні відмінності. Однак початок і там і там було покладено однаково. Першою дробом стала половина або 1/2. Далі виникла чверть, третину і так далі. Згідно з даними археологічних розкопок, історія виникнення дробів налічує близько 5 тисяч років. Вперше частки числа зустрічаються в єгипетських папірусах і на вавилонських глиняних табличках. Система числення в Вавилоні була Шістдесяткова. Кожен новий розряд відрізнявся від попереднього на 60. Така система збереглася в сучасному світі для позначення часу і величин кутів. Дробу також були шістдесяткова. Для запису використовували спеціальні значки. Як і в Єгипті, приклади з дробом містили окремі символи для позначення 1/2, 1/3 і 2/3. Вавилонська система не зникла разом з державою. Дробом, написаними в 60-тірічной системі, користувалися античні і арабські астрономи і математики.Колись дії зі звичайними дробами завдавали людям надзвичайних труднощів. Ці труднощі у Вавилоні пояснювали "втручанням злих духів". Англійський чернець Бєда, який був ученою людиною свого часу, писав у VII сторіччі: "У світі є багато речей, але немає нічого важчого, як чотири дії арифметики". Тоді ж, мабуть, і виникла німецька приказка "попасти в дроби", що означала опинитися у скрутному становищі. А причина, звичайно, полягала в тому, що не було встановлено загальних правил виконання дій з дробами, не було створено відповідної теорії.
Дроби у давньому Римі
Римська система дробів була пов'язана з мірою ваги, званої «асс». Вона ділилася на 12 часток. 1/12 асса називалася унцією. Для позначення дробів існувало 18 назв. Наведемо деякі з них:семис — половина асса; секстанте — шоста частка асса; семиунция — пів-унції або 1/24 асса. Незручність такої системи полягала в неможливості подати число у вигляді дробу зі знаменником 10 або 100. Римські математики подолали труднощі з допомогою використання відсотків.

Застосування звичайних дробів
Звичайні дроби застосовуються:Звичайні дроби в промисловості.Дроби і здоров'я людини.Дроби у повсякденному житті.Звичайні дроби і музика.
a
Застосування звичайних дробів у математичних задачах
1. Ділення на частки: Наприклад, якщо у вас є 12 яблук, і ви хочете розділити їх між 3 дітьми порівну, ви можете використовувати звичайні дроби, щоб виразити кількість яблук для кожної дитини як 12/3 = 4.2. Поділ на частини: Наприклад, якщо у вас є піца, розділена на 8 шматків, і ви хочете з'їсти половину піци, ви можете використовувати звичайні дроби, щоб виразити кількість шматків, які вам потрібно з'їсти, як 1/2 * 8 = 4.3. Порівняння кількостей: Наприклад, якщо у вас є 3/4 пляшки соку і 2/3 пляшки лимонаду, ви можете використовувати звичайні дроби, щоб порівняти кількості напоїв і визначити, який більше.4. Розрахунок вартості: Наприклад, якщо ціна однієї книги становить 1/2 долара, а ви хочете купити 3 книги, ви можете використовувати звичайні дроби, щоб обчислити загальну вартість як 1/2 * 3 = 1.5 долара.5. Розрахунок відсотків: Наприклад, якщо ви отримали 4 з 10 правильних відповідей на тесті, ви можете використовувати звичайні дроби, щоб обчислити відсоток правильних відповідей як 4/10 * 100% = 40%.

Перетворення звичайних дробів
Перетворення звичайних дробів включає розкладання на прості дроби, зведення до спільного знаменника та перетворення змішаних чисел на неправильні дроби. Ось кілька прикладів перетворень звичайних дробів:1. Розкладання на прості дроби: Наприклад, якщо маємо дріб 3/8, можемо розкласти його на прості дроби шляхом знаходження спільного дільника для чисельника і знаменника. У цьому випадку, 3 і 8 не мають спільних дільників, тому 3/8 є простою дробом.2. Зведення до спільного знаменника: Наприклад, якщо маємо дроби 2/3 і 3/4, можемо звести їх до спільного знаменника, який у цьому випадку буде 12. Перетворюємо дроби: 2/3 = 8/12 (помножуємо чисельник і знаменник першого дробу на 4) 3/4 = 9/12 (помножуємо чисельник і знаменник другого дробу на 3) Тепер можемо виконати операції з дробами, оскільки вони мають однаковий знаменник.3. Перетворення змішаних чисел на неправильні дроби: Наприклад, якщо маємо змішане число 1 3/4, можемо перетворити його на неправильний дріб, обчисливши його значення. У цьому випадку, 1 3/4 можна розглядати як 4/4 + 3/4 = 7/4.Це лише кілька прикладів перетворень звичайних дробів. Зверніть увагу, що в деяких випадках можуть бути застосовані інші методи та правила для перетворень дробів, залежно від конкретної ситуації.
Перетворення неправильних дробів в мішані числа
Для перетворення неправильного дробу в мішане число необхідно:поділити чисельник дробу на його знаменник;остачу від ділення записати в чисельник, знаменник залишити без змін;результат від ділення записати в якості цілої частини.
Перетворення десяткових дробів в звичайні дроби.
Щоб перетворити десятковий дріб в звичайний дріб, потрібно представити його дробову частину у вигляді натурального числа, поділеного на 10 в відповідній степені. Після чого спростити отриманий дріб і до результату приписати цілу частину з відповідним знаком, формуючи мішаний дріб.
aПеретворення мішаних дробів в неправильні дроби.
Щоб представити мішане число у вигляді неправильного дробу, потрібно:помножити його цілу частину на знаменник дробової частини;до отриманого добутку додати чисельник дробової частини;записати отриману суму чисельником дробу, а знаменник дробової частини залишити без зміни.