Asíntota vertical

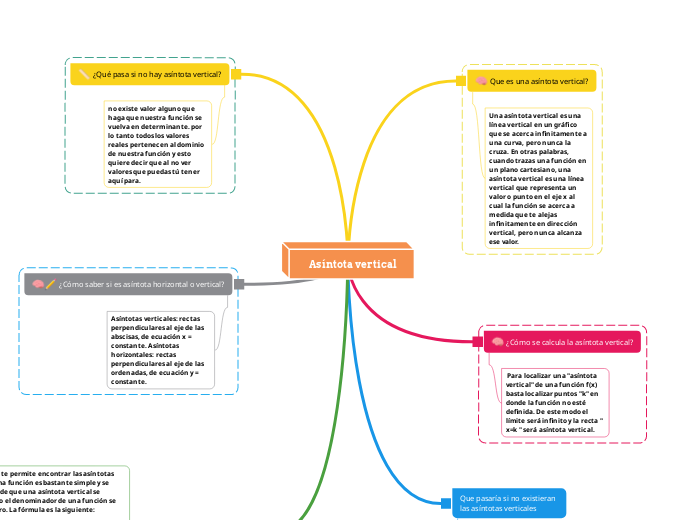
Que es una asíntota vertical?

Una asíntota vertical es una línea vertical en un gráfico que se acerca infinitamente a una curva, pero nunca la cruza. En otras palabras, cuando trazas una función en un plano cartesiano, una asíntota vertical es una línea vertical que representa un valor o punto en el eje x al cual la función se acerca a medida que te alejas infinitamente en dirección vertical, pero nunca alcanza ese valor.

¿Cómo se calcula la asíntota vertical?

Para localizar una "asíntota vertical" de una función f(x) basta localizar puntos "k" en donde la función no esté definida. De este modo el límite será infinito y la recta " x=k " será asíntota vertical.

Que pasaría si no existieran las asíntotas verticales

Si no existieran las asíntotas verticales en el contexto de funciones racionales y otros tipos de funciones, habría algunas consecuencias importantes:

Pérdida de información sobre el comportamiento de las funciones

Dificultad en el análisis de gráficos

¿Qué pasa si no hay asíntota vertical?

no existe valor alguno que haga que nuestra función se vuelva en determinante. por lo tanto todos los valores reales pertenecen al dominio de nuestra función y esto quiere decir que al no ver valores que puedas tú tener aquí para.

¿Cómo saber si es asíntota horizontal o vertical?

Asíntotas verticales: rectas perpendiculares al eje de las abscisas, de ecuación x = constante. Asíntotas horizontales: rectas perpendiculares al eje de las ordenadas, de ecuación y = constante.

Formula de Asíntota vertical

La fórmula que te permite encontrar las asíntotas verticales de una función es bastante simple y se basa en la idea de que una asíntota vertical se produce cuando el denominador de una función se hace igual a cero. La fórmula es la siguiente:

Dado una función racional de la forma f(x) = g(x) / h(x), las asíntotas verticales ocurren cuando el denominador h(x) se hace igual a cero, pero el numerador g(x) no se anula en ese punto. Por lo tanto, para encontrar las asíntotas verticales, necesitas resolver la siguiente ecuación:

h(x) = 0