Asíntota vertical
¿Que es?

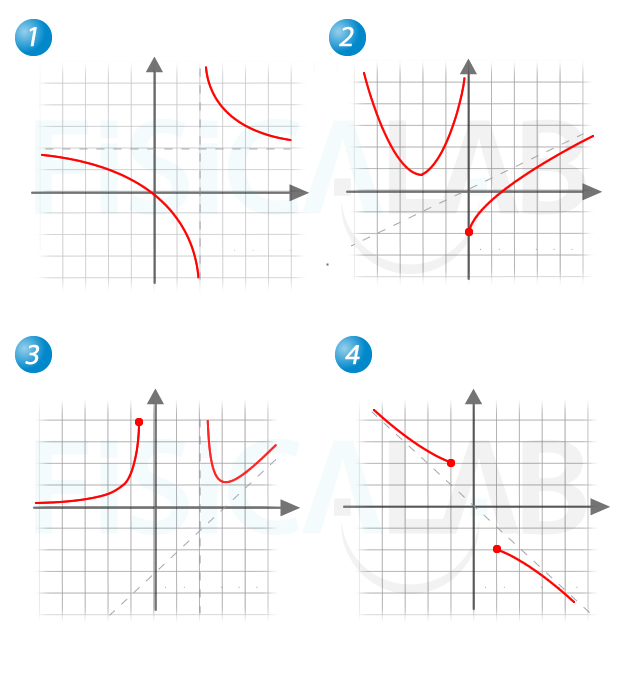
Tipos de asíntota
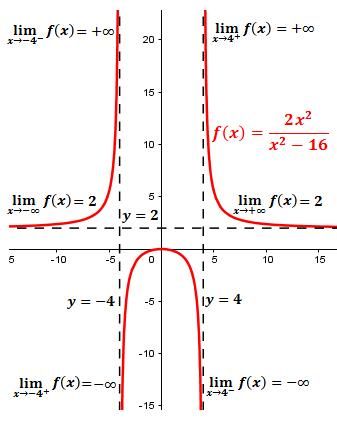

¿Es posible que una función tenga más de una asíntota vertical?
Sí, es posible. Un ejemplo es la función
𝑓(𝑥)=1/(𝑥−1)(𝑥+2) , que tiene asíntotas verticales en
x=1 y x=−2. Esto se debe a que el denominador se anula en esos puntos, causando que la función tienda a infinito.
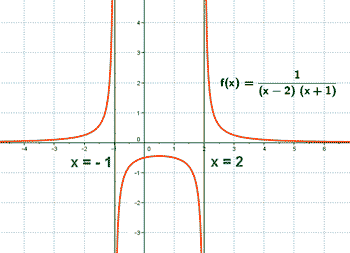
Historia y significado

Cálculo de asíntota vertical por medio de límites
La recta x= a , es una astintota vertical de la grafica de la funcion al menos uno de los siguientes enunciados verdadero:
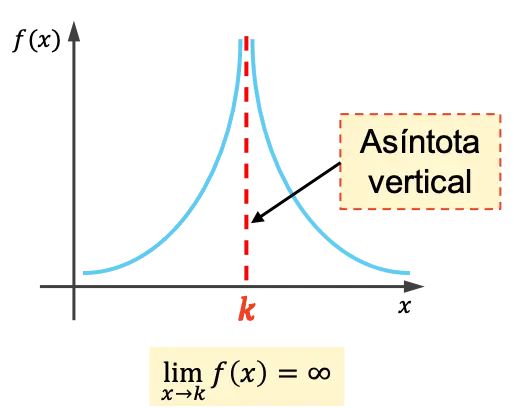
¿Qué técnicas gráficas pueden utilizarse para identificar asíntotas verticales en una función?