MATEMÁTICA BÁSICA

¿Que es un conjunto? Es un grupo de elementos u objetos especificados en tal forma que se puede afirmar con certeza si cualquier objeto dado pertenece o no a la agrupación. Para denotar a los conjuntos, se usan letras mayúsculas.

Cuando un elemento x pertenece a un conjunto A se expresa de forma simbólica como: x ∈ A . En caso de que un elemento y no pertenezca a este mismo conjunto se utiliza la notación: y ∉ A

FORMAS DE CONJUNTOS

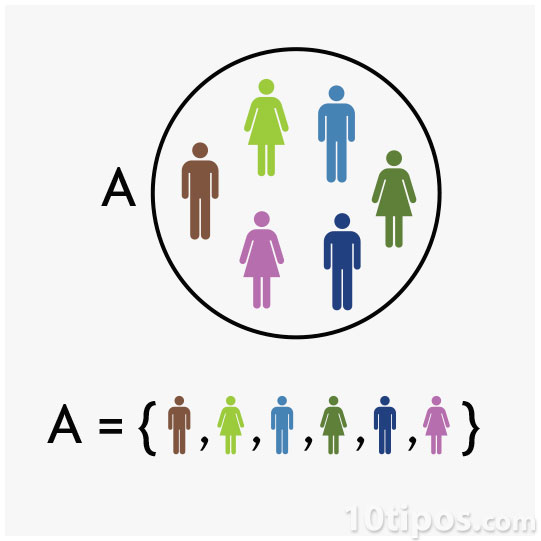
1) Por extensión o enumeración: los elementos son encerrados entre llaves y separados por comas. Es decir, el conjunto se describe listando todos sus elementos entre llaves.

2) Por comprensión: los elementos se determinan a través de una condición que se establece
entre llaves. En este caso se emplea el símbolo | que significa “tal que". En forma simbólica es:
A = { x P(x) }= {x1, x2, x3, ⋅⋅⋅ xn }
que significa que el conjunto A es el conjunto de todos los elementos x tales que la condición P(x) es verdadera, como x1, x2, x3... , etc.

3) Diagramas de Venn: son regiones cerradas que sirven para visualizar el contenido de un
conjunto o las relaciones entre conjuntos.

4) Por descripción verbal: Es un enunciado que describe la característica que es común para los
elementos.

OPERECIONES

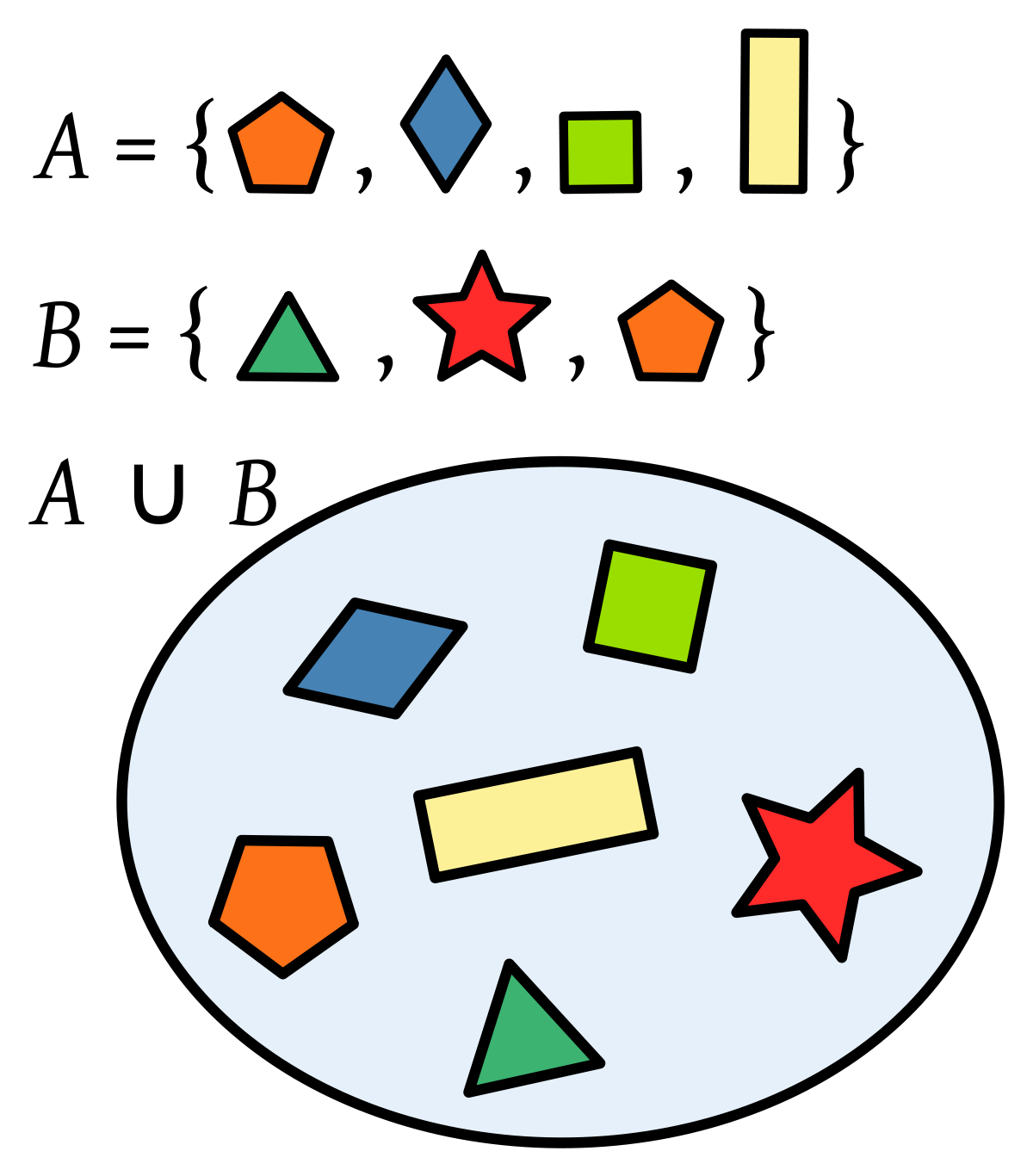
La unión de los conjuntos A y B es el conjunto de todos los elementos de A con todos los
elementos de B sin repetir ninguno y se denota como A∪ B . Esto es:
A∪ B = { x x ∈ A o x ∈ B }

UNION

Propiedades asociativas, si en una unión de tres o más conjuntos se reemplazan dos conjuntos por su unión efectuada, se obtiene el mismo resultado.
R∩S∩T=(R∩S)∩T
R∩S∩T=R∩(S∩T)

Propiedades conmutativas, Si en una unión se altera el orden de los conjuntos, el resultado no varía.
R∪S∪T=S∪R∪T
R∪S∪T=T∪R∪S

INTERSECCIÓN

Propiedad asociativa, si en una intersección de tres o más conjuntos se reemplazan dos de ellos por su intersección efectuada, el resultado total es el mismo.
R∪S∪T=(R∪S)∪T
R∪S∪T=R∪(S∪T)

Propiedad conmutativa, cambiando el orden de los conjuntos, la intersección no se altera.
R∩S∩T=R∩T∩S
R∩S∩T=T∩R∩S

Propiedad distributiva

La unión es distributiva con respecto a la intersección.
(R∩S)∪T=(R∪T)∩(S∪T)

La intersección de conjuntos es distributiva con respecto a la unión.
(R∪S)∩T=(R∩T)∪(S∩T)

Establecen los complementos de la unión e intersección entre conjuntos.

PRIMERA LEY: El complemento de la ley unión de dos conjuntos es la intersección de sus complementos. (A U B)' = A' n B'

EJEMPLO

xϵ(AnB)' = x∉AnB
1. x∉A ∧ xϵB = x ϵ A'
2. xϵA ∧ x∉B = xϵB'
x ϵ A' ∨ x ϵ B'
A'uB' = (AnB)'

Segunda ley: El complemento de la intersección de dos conjuntos es la unión de sus complementos: (AuB)' = A'nB'

EJEMPLO

U={1,2,3,4,5,6,7,8,9,10,11,12}
A={1,3,4,7,9,11}
B={1,2,5,7,9,11,12}
AUB={1,2,3,4,5,6,7,8,9,10,11,12}
(AUB)'= {6,8,10}


A'={2,5,6,8,10,12}
B'={3,4,6,8,10}
A'nB'={6,8,10}

Las dos operaciones nos entregan exactamente lo mismo.

también conocidas como álgebra de conjuntos, nos permiten realizar operaciones sobre los conjuntos para obtener otro conjunto.

UNION O REUNION DE CONJUNTOS

Es la operación que nos permite unir dos o más conjuntos para formar otro conjunto que contendrá a todos los elementos que queremos unir pero sin que se repitan

El símbolo que se usa para indicar la operación de unión es el siguiente: ∪. Cuando usamos diagramas de Venn, para representar la unió de conjuntos, se sombrean los conjuntos que se unen o se forma uno nuevo. Luego se escribe por fuera la operación de unión.

EJEMPLO

Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la unión de estos conjuntos será A∪B={1,2,3,4,5,6,7,8,9}. Usando diagramas de Venn se tendría lo siguiente:

INTERSECCIÓN DE CONJUNTOS

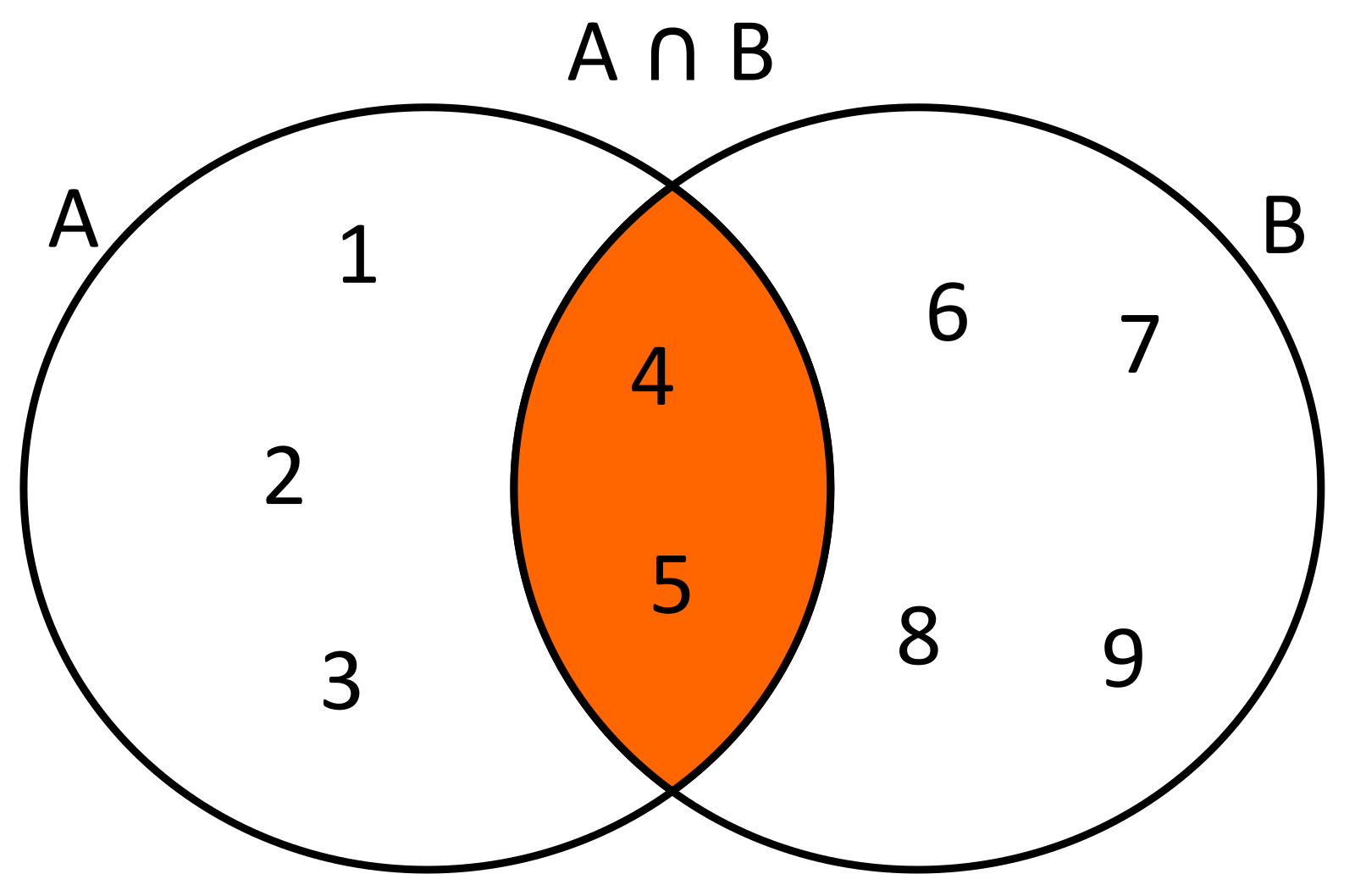
Es la operación que nos permite formar un conjunto, sólo con los elementos comunes involucrados en la operación. Es decir dados dos conjuntos A y B, la de intersección de los conjuntos A y B, estará formado por los elementos de A y los elementos de B que sean comunes, los elementos no comunes A y B, será excluidos. El símbolo que se usa para indicar la operación de intersección es el siguiente: ∩.

EJEMPLO

Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la intersección de estos conjuntos será A∩B={4,5}. Usando diagramas de Venn se tendría lo siguiente:

DIFRENCIA DE SIMETRICA DE CONJUNTOS

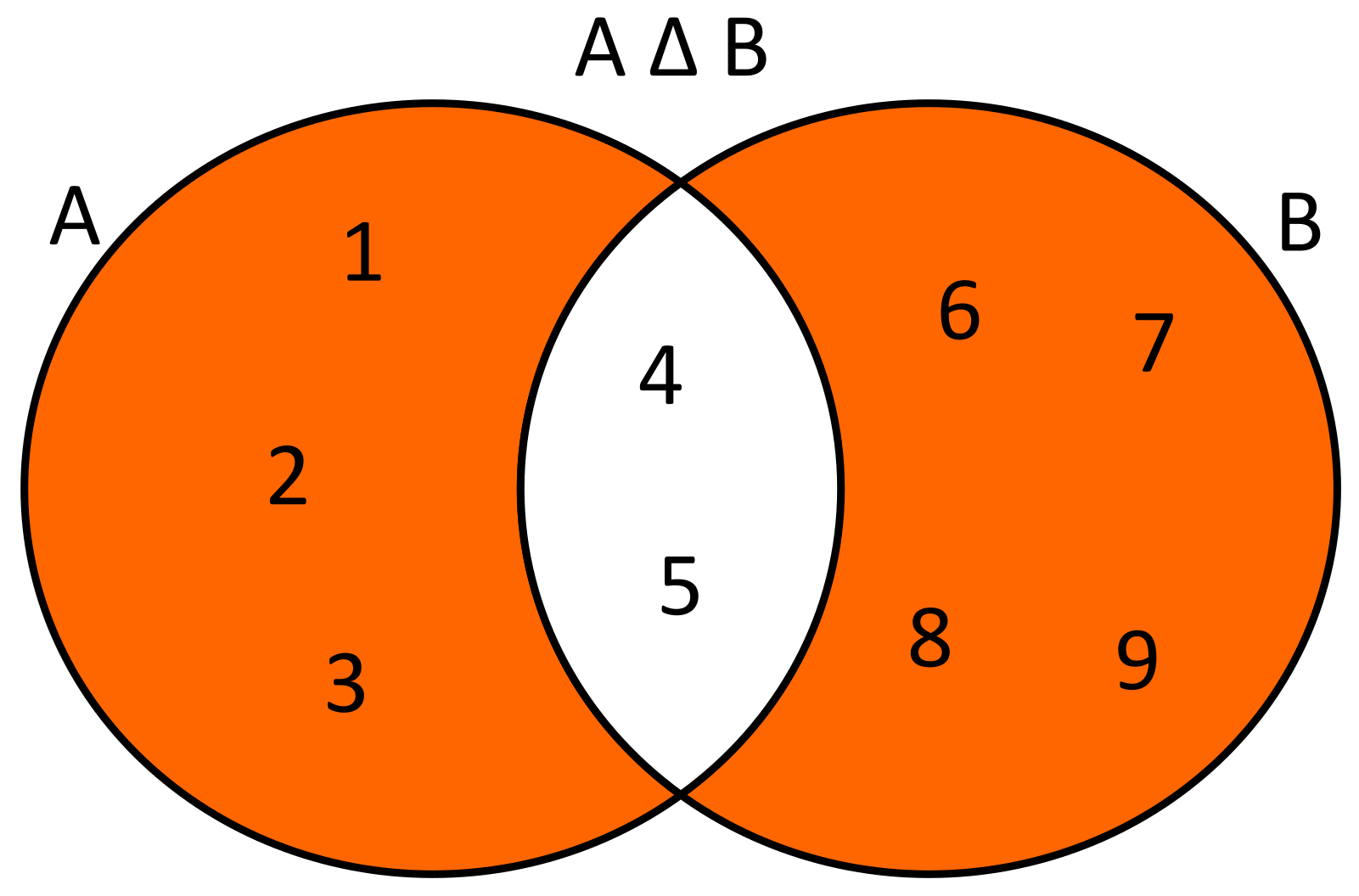
Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que tendrá todos los elementos que no sean comunes a ambos conjuntos. Es decir dados dos conjuntos A y B, la diferencia simétrica estará formado por todos los elementos no comunes a los conjuntos A y B. El símbolo que se usa para indicar la operación de diferencia simétrica es el siguiente: △.

EJEMPLO

Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia simétrica de estos conjuntos será A △ B={1,2,3,6,7,8,9}. Usando diagramas de Venn se tendría lo siguiente:

DIFERENCIA DE CONJUNTOS

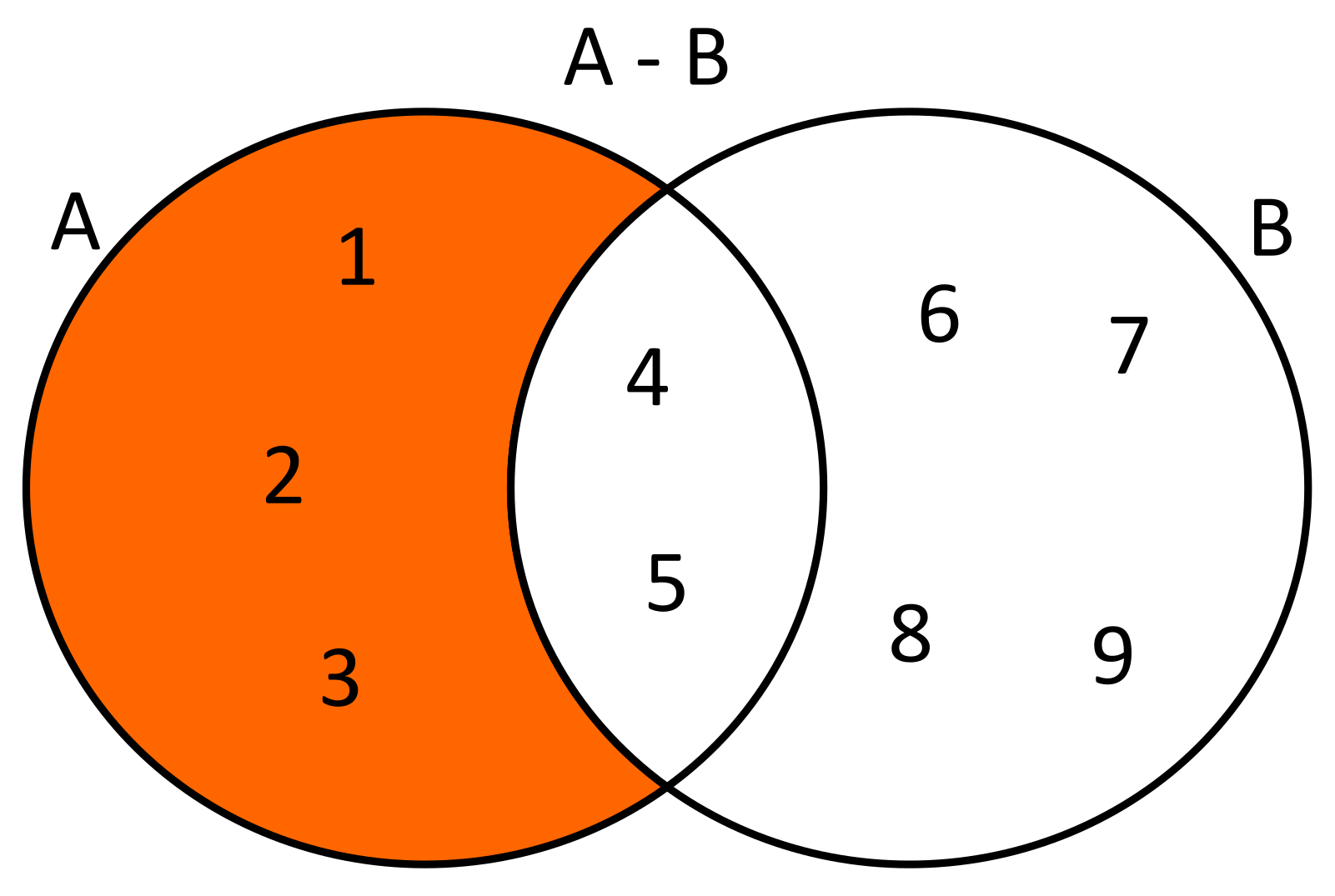
Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que tendrá todos los elementos que pertenecen al primero pero no al segundo. Es decir dados dos conjuntos A y B, la diferencia de los conjuntos entra A y B, estará formado por todos los elementos de A que no pertenezcan a B. El símbolo que se usa para esta operación es el mismo que se usa para la resta o sustracción, que es el siguiente: -.

EJEMPLO

Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia de estos conjuntos será A-B={1,2,3}. Usando diagramas de Venn se tendría lo siguiente:

COMPLEMENTO DE UN CONJUNTO

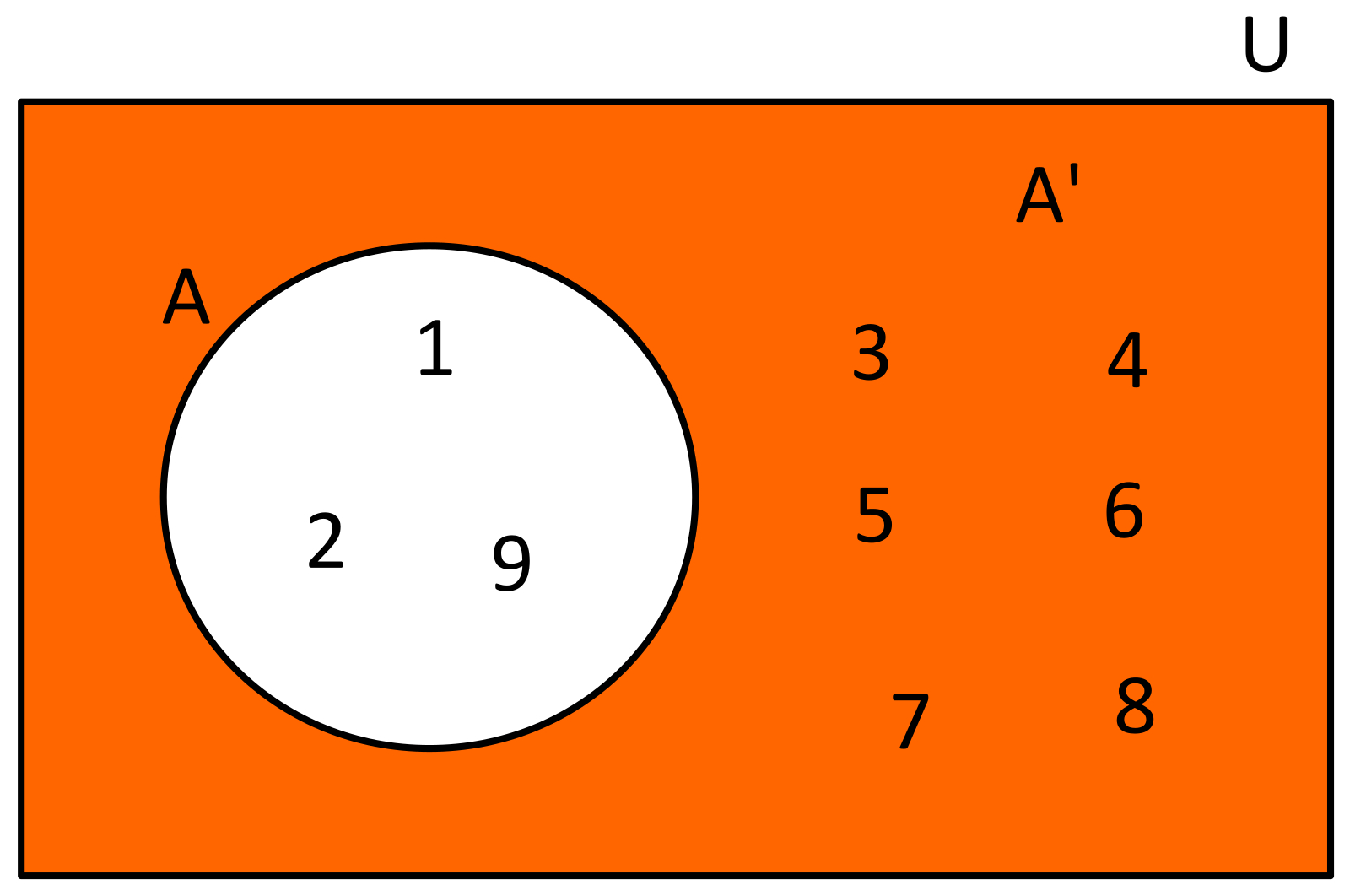
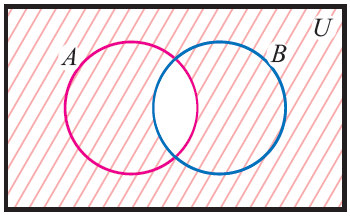
Es la operación que nos permite formar un conjunto con todos los elementos del conjunto de referencia o universal, que no están en el conjunto. Es decir dado un conjunto A que esta incluido en el conjunto universal U, entonces el conjunto complemento de A es el conjunto formado por todos los elementos del conjunto universal pero sin considerar a los elementos que pertenezcan al conjunto A. En esta operación el complemento de un conjunto se denota con un apostrofe sobre el conjunto que se opera, algo como esto A' en donde el el conjunto A es el conjunto del cual se hace la operación de complemento.

EJEMPLO

Dado el conjunto Universal U={1,2,3,4,5,6,7,8,9} y el conjunto A={1,2,9}, el conjunto A' estará formado por los siguientes elementos A'={3,4,5,6,7,8}. Usando diagramas de Venn se tendría lo siguiente: