ПОХІДНА
Означення
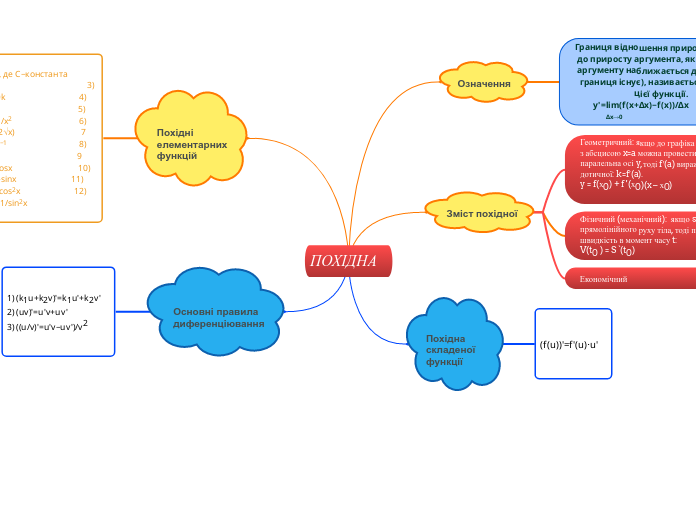
Границя відношення приросту функції до приросту аргумента, якщо приріст аргументу наближається до нуля (і ця границя існує), називається похідною цієї функції.
y'=lim(f(x+Δx)−f(x))/Δx Δx→0
Зміст похідної
Геометричний: якщо до графіка функції y=f(x) в точці з абсцисою x=a можна провести дотичну, яка не паралельна осі y, тоді f′(a) виражає кутовий коефіцієнт дотичної: k=f′(a). y = f(х0) + f '(х0)(x – х0)
Фізичний (механічний): якщо s(t) - закон прямолінійного руху тіла, тоді похідна виражає миттєву швидкість в момент часу t:
V(t0 ) = S `(t0)