Estadísticas. De: Alexis Omar Dorado Dávila

Distribución Numérica

Una distribución de frecuencia es una tabulación o representación gráfica que muestra la frecuencia de ocurrencia de diferentes valores en un conjunto de datos. Se utiliza para resumir y visualizar datos, y para identificar patrones y tendencias.

Distribuciones de frecuencia agrupadas: muestran la frecuencia de rangos de valores en un conjunto de datos. Se utilizan cuando hay un gran número de valores diferentes en el conjunto de datos.

Distribuciones de frecuencia agrupadas: muestran la frecuencia de rangos de valores en un conjunto de datos. Se utilizan cuando hay un gran número de valores diferentes en el conjunto de datos.

Indican la ubicación de un valor dentro de un conjunto de datos ordenado. Las medidas de posición más comunes son:
Media (promedio): Suma de todos los valores dividida por la cantidad de valores.
Mediana: Valor que divide al conjunto de datos ordenado en dos mitades iguales.
Moda: Valor que aparece con mayor frecuencia.

En estadística, una distribución categórica (también llamada distribución de Bernoulli generalizada o distribución multinomial) es una distribución de probabilidad discreta que describe los posibles resultados de una variable aleatoria que puede tomar una de K categorías posibles. La probabilidad de cada categoría se especifica por separado.

Variable aleatoria: La variable aleatoria asociada a una distribución categórica se denomina variable categórica.

Valores posibles: La variable categórica puede tomar K valores diferentes, donde K es un número finito.

Probabilidades: Cada categoría tiene una probabilidad asociada, P(k), donde k = 1, 2, ..., K.

Restricciones: Las probabilidades de todas las categorías deben sumar 1: Σ P(k) = 1.

En estadística, la función de distribución acumulada (FDC), también llamada distribución acumulada, es una función que describe la probabilidad de que una variable aleatoria sea menor o igual que un valor específico.

Concepto

Es la ciencia que se ocupa de la recopilación, organización, análisis, interpretación y presentación de datos. Se utiliza para tomar decisiones informadas en una amplia variedad de campos, incluidos los negocios, la ciencia, la ingeniería y el gobierno.

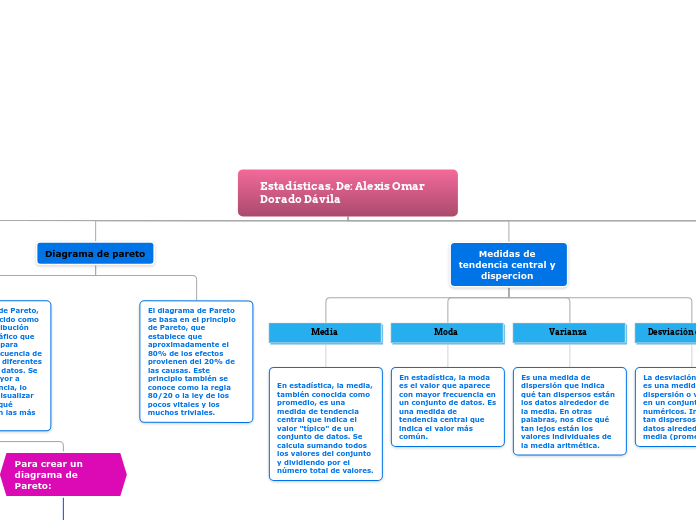
Diagrama de pareto

Un diagrama de Pareto, también conocido como curva de distribución ABC, es un gráfico que utiliza barras para mostrar la frecuencia de ocurrencia de diferentes categorías de datos. Se ordena de mayor a menor frecuencia, lo que permite visualizar rápidamente qué categorías son las más importantes.

Identificar las causas más importantes de un problema.
Priorizar la mejora de procesos.
Tomar decisiones sobre la asignación de recursos.

Identifique el problema o proceso que desea analizar.
Recopile datos sobre las diferentes categorías de causas o efectos.
Ordene las categorías de mayor a menor frecuencia.
Calcule el porcentaje acumulativo de frecuencia para cada categoría.
Cree un gráfico de barras con las categorías en el eje horizontal y la frecuencia o el porcentaje acumulativo en el eje vertical.

El diagrama de Pareto se basa en el principio de Pareto, que establece que aproximadamente el 80% de los efectos provienen del 20% de las causas. Este principio también se conoce como la regla 80/20 o la ley de los pocos vitales y los muchos triviales.

Medidas de tendencia central y dispercion

En estadística, la media, también conocida como promedio, es una medida de tendencia central que indica el valor "típico" de un conjunto de datos. Se calcula sumando todos los valores del conjunto y dividiendo por el número total de valores.

En estadística, la moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Es una medida de tendencia central que indica el valor más común.

Es una medida de dispersión que indica qué tan dispersos están los datos alrededor de la media. En otras palabras, nos dice qué tan lejos están los valores individuales de la media aritmética.

La desviación estándar es una medida de dispersión o variabilidad en un conjunto de datos numéricos. Indica qué tan dispersos están los datos alrededor de la media (promedio).

diagrama de dispercion

Un diagrama de dispersión es un tipo de gráfico que muestra la relación entre dos variables. Se crea trazando puntos en un plano cartesiano, donde cada punto representa un valor para cada variable.

Visualizar la relación entre dos variables.
Determinar si existe una correlación entre dos variables.
Estimar la fuerza de la correlación entre dos variables.

Identifique las dos variables que desea graficar.
Etiquete el eje X con la variable independiente.
Etiquete el eje Y con la variable dependiente.
Trace un punto para cada par de valores de datos.

Histogramas

Un histograma es una representación gráfica de la distribución de una variable cuantitativa. Se construye dividiendo el rango de valores en intervalos y luego contando el número de datos que caen en cada intervalo. La altura de cada barra en el histograma es proporcional a la frecuencia de datos en el intervalo correspondiente.

Características clave de un histograma:

El eje horizontal muestra los intervalos de valores.
El eje vertical muestra la frecuencia de datos.
Las barras son adyacentes y no hay espacios entre ellas.
La forma del histograma proporciona información sobre la forma de la distribución de los datos.

Los histogramas se pueden usar para:

Visualizar la distribución de una variable.
Identificar valores atípicos.
Comparar dos o más conjuntos de datos.
Hacer inferencias sobre la población a partir de una muestr

Polígono de frecuencia

Un polígono de frecuencia es un gráfico que muestra la frecuencia de una variable cuantitativa. Se crea conectando los puntos medios de las barras de un histograma.

El eje horizontal muestra los valores de la variable.
El eje vertical muestra la frecuencia de datos.
Los puntos están conectados por segmentos de línea.
La forma del polígono proporciona información sobre la forma de la distribución de los datos.

Visualizar la distribución de una variable.
Identificar valores atípicos.
Comparar dos o más conjuntos de datos.
Hacer inferencias sobre la población a partir de una muestra.