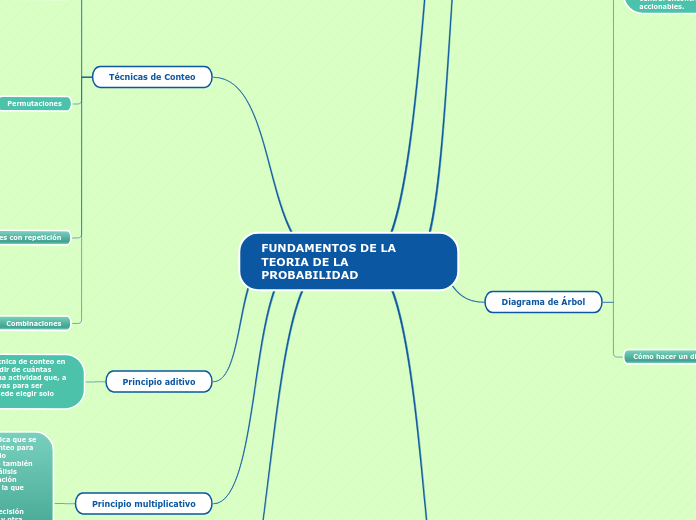
FUNDAMENTOS DE LA TEORIA DE LA PROBABILIDAD
Permutaciones
En matemáticas, una permutación es la variación del orden o posición de los elementos de un conjunto ordenado o una tupla. La definición intuitiva de permutación, como un ordenamiento de los elementos de un conjunto se formaliza con el uso del lenguaje de funciones matemáticas.
Combinaciones
La combinatoria es una rama de la matemática perteneciente al área de matemáticas discretas que estudia la enumeración, construcción y existencia de propiedades de configuraciones que satisfacen ciertas condiciones establecidas. Además, estudia las ordenaciones o agrupaciones de un determinado número de elementos.
Los aspectos de la combinatoria incluyen contar las estructuras de un tipo y tamaño dado (combinatorias enumerativas), decidir cuándo pueden cumplirse ciertos criterios y construir y analizar objetos que cumplan los criterios (como en los diseños combinatorios y la teoría de matroides) encontrar objetos "más grandes", "más pequeños" u "óptimos" (combinatoria extrema y optimización combinatoria), estudiar estructuras combinatorias surgidas en un contexto algebraico, o aplicar técnicas algebraicas a problemas combinatorios (combinatoria algebraica)
Diagrama de Árbol
Es una herramienta de calidad que a través de un proceso sistemático nos permite hallar la relación existente entre un concepto general y los elementos que lo componen. Parte de un elemento central (tronco) que se desagrega en otros subelementos más pequeños (ramas de primer nivel), que a su vez también se desagregan en otros elementos; de ahí el nombre de árbol. Así pues, en la medida en que vamos desagregando el elemento central encontramos medios más detallados y accionables.
Cómo hacer un diagrama de árbol
Paso 1: Definiendo el grupo de trabajo
Puedes hacerlo solo, pero según la complejidad de la situación que se aborda es posible que no obtengas los mejores resultados. De ahí que para hacer un diagrama de árbol siempre sea mejor definir un equipo de trabajo.
Deberá haber personas con conocimiento de la situación que se aborda, también personal con capacidad analítica y de diferentes áreas de conocimiento si es aplicable.
Paso 2: Definiendo el elemento central
Toda desagregación tiene un punto de partida general, defínelo. Este será el problema, situación, meta, proyecto o lo que sea que vamos a desagregar. Puedes ubicarlo en la parte superior del diagrama desde donde se empezará a desagregar, o lo que es más común, a la izquierda de todo.
Paso 3: Las ramas de primer nivel
Consideramos que al tener completos los medios o ramas de primer nivel lograremos dar solución al elemento central. Puede que al ser el primer nivel estemos algo confundidos al no saber cómo empezar. Conviene entonces que nos preguntemos:
Si hablamos de un proyecto, objetivo o plan de acción: ¿Qué tenemos qué hacer para lograr esto? o «Para conseguir esto, debemos…»
Si hablamos de un proyecto: ¿Qué es lo que está causando este problema? o ¿Por qué se está generando esto?
Y si es un producto: ¿Cómo podemos descomponer la elaboración de este producto?
Como ves, todo sigue el mismo procedimiento independiente del caso.
Todo se logra a través de una lluvia de ideas, pero también te será util, si lo tienes de antes, los elementos obtenidos en un diagrama de relaciones o diagrama de afinidad.
Paso 4: Primer verificación
Ya con el primer nivel desagregado, en este paso nos aseguramos de que no nos falte nada.
Pregúntate entonces:
¿Teniendo completas todos los elementos, conseguimos cumplir el elemento central?
¿Son necesarios todos estos elementos para cumplir el elemento central?
Paso 5: Repetimos paso 3 y 4.
Es decir que los elementos detectados en el nivel anterior, serán objetivo de la pregunta
Paso 6: Verificación final
Con esta verificación tomamos todos los elementos desde la parte inferior del árbol y comenzamos a subir por cada nivel, hasta que comprobar que en efecto, no sobran ni faltan elementos para completar el elemento central.
Subtopic
Teorema del Binomio
El teorema del binomio es una ecuación que nos dice cómo se desarrolla una expresión de la forma (a+b)n para algún número natural n. Un binomio no es más que la suma de dos elementos, como (a+b). También nos permite saber para un término dado por akbn-k cuál es el coeficiente que lo acompaña. Este teorema es comúnmente atribuido al inventor, físico y matemático inglés Sir Isaac Newton; sin embargo, se han encontrado diversos registros que indican que en el Medio Oriente ya se conocía su existencia, alrededor del año 1000.
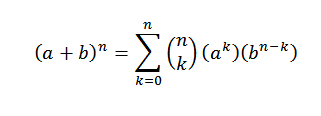
Técnicas de Conteo
Principio multiplicativo
Este tipo de técnica de conteo, junto con el principio aditivo, permiten comprender fácilmente y de forma práctica cómo funcionan estos métodos matemáticos.
Si un evento, llamemoslo N1, puede ocurrir de varias formas, y otro evento, N2, puede ocurrir de otras tantas, entonces, los eventos conjuntamente pueden ocurrir de N1 x N2 formas.
Este principio se utiliza cuando la acción es secuencial, es decir, está conformada por eventos que ocurren de forma ordenada, como son la construcción de una casa, el elegir los pasos de baile en una discoteca o el orden que se seguirá para preparar un pastel
Principio aditivo
En este caso, en vez de multiplicarse las alternativas para cada evento, lo que sucede es que se suman las varias formas en las que pueden ocurrir.
Esto quiere decir que si la primera actividad puede ocurrir de M formas, la segunda de N y la tercera L, entonces, de acuerdo a este principio, sería M + N + L.
Permutaciones
Antes de entender cómo hacer las permutaciones, es importante entender la diferencia entre una combinación y una permutación.
Una combinación es un arreglo de elementos cuyo orden no es importante o no cambia el resultado final.
En cambio, en una permutación, habría un arreglo de varios elementos en los que sí es importante tenerse en cuenta su orden o posición.
En las permutaciones, hay n cantidad de elementos distintos y se selecciona una cantidad de ellos, que sería r.
La fórmula que se utilizaría sería la siguiente: nPr = n!/(n-r)!
Permutaciones con repetición
Cuando se quiere saber el número de permutaciones en un conjunto de objetos, algunos de los cuales son iguales, se procede a realizar lo siguiente:
Teniéndose en cuenta que n son los elementos disponibles, algunos de ellos repetidos.
Se seleccionan todos los elementos n.
Se aplica la siguiente fórmula: = n!/n1!n2!...nk!
Combinaciones
En las combinaciones, a diferencia de lo que sucedía con las permutaciones, el orden de los elementos no es importante.
La fórmula a aplicar es la siguiente: nCr=n!/(n-r)!r!
Principio aditivo
El principio aditivo es una técnica de conteo en probabilidad que permite medir de cuántas maneras se puede realizar una actividad que, a su vez, tiene varias alternativas para ser realizada, de las cuales se puede elegir solo una a la vez.
Principio multiplicativo
El principio multiplicativo es una técnica que se utiliza para resolver problemas de conteo para hallar la solución sin que sea necesario enumerar sus elementos. Es conocido también como el principio fundamental del análisis combinatorio; se basa en la multiplicación sucesiva para determinar la forma en la que puede ocurrir un evento.
Este principio establece que, si una decisión (d1) puede ser tomada de n maneras y otra decisión (d2) puede tomarse de m maneras, el número total de maneras en las que pueden ser tomadas las decisiones d1 y d2 será igual a multiplicar de n * m. Según el principio, cada decisión se realiza una tras otra: número de maneras = N1 * N2… * Nx maneras

Training
Notación Factorial.
La notación factorial se usa para calcular el producto de los primeros n números naturales, es decir, los enteros positivos, comenzando desde el 1 hasta el valor de n. Se denota mediante un signo de admiración y se llama n factorial: n! = 1⋅2⋅3…. (n-1)⋅n
Calcular el factorial de un número es sencillo, por ejemplo, el producto de los seis primeros números naturales se expresa mediante:
6! = 1⋅2⋅3⋅4⋅5⋅6 = 720