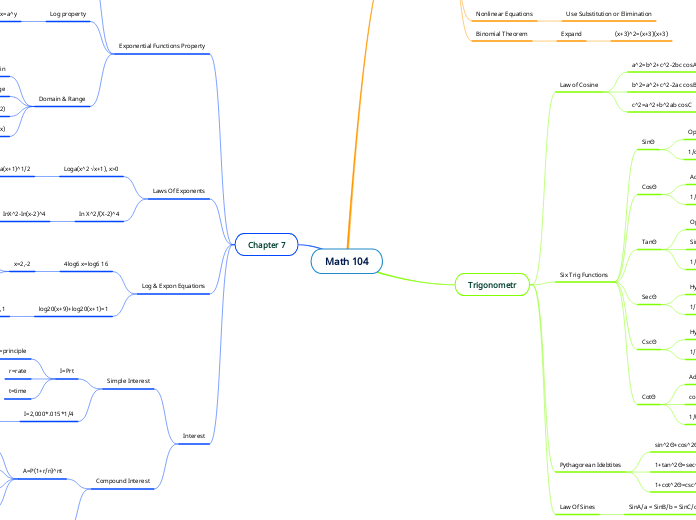
Math 104

Systems Of Equations

Consistent, Inconsistent, And Dependent

Matrices

Augmented Matrix

Row Echelon Form

Determinants

Cramer's Rules

2x2 Determinats

3x3 Determinants

Nonlinear Equations

Use Substitution or Elimination

Binomial Theorem

Expand

(x+3)^2=(x+3)(x+3)

Law of Cosine

a^2=b^2+c^2-2bc cosA

b^2=a^2+c^2-2ac cosB

c^2=a^2+b^2ab cosC

Six Trig Functions

SinΘ

Opposite/Hypotenuse

1/cscΘ

CosΘ

Adjacent/ Hypotenuse

1/secΘ

TanΘ

Opposite/Adjacent

SinΘ/cosΘ

1/cotΘ

SecΘ

Hypotenuse/Adjacent

1/cosΘ

CscΘ

Hypotenuse/Opposite

1/sinΘ

CotΘ

Adjacent/Opposite

cosΘ/sinΘ

1/tanΘ

Pythagorean Idebtites

sin^2Θ+cos^2Θ=1

1+tan^2Θ=sec^2Θ

1+cot^2Θ=csc^2Θ

Law Of Sines

SinA/a = SinB/b = SinC/c

Exponential Functions Property

a^u=a^v ↔ u=v

Log property

y=logx ↔ x=a^y

y=log7x ↔ x=7^y

1.6^3= ↔ 3=log1.6

e^u=25 ↔ u=loge25

log3 81 ↔ y=log3 81

y=4

Domain & Range

Domain

(0,∞)

Cant have zero so its not included

Range

(∞,∞)

f(x)=log3(x+2)

Domain: {x|X>-2}

Interval Notation: (-2,∞)

g(x)=log(5+x/5-x)

Interval Notation: (-5,5)

Laws Of Exponents

Loga(x^2 √x+1), x>0

2logax+loga(x+1)^1/2

2logax+1/2loga(x+1)

"Express All powers as factors"

All powers= Exponents

In X^2/(X-2)^4

InX^2-In(x-2)^4

2Inx-4In(x-2)

"Express all powers as factors"

All powers= Exponents

Log & Expon Equations

4log6 x=log6 16

x=2,-2

"x cant be negative"

Final Answer: x=2

log20(x+9)+log20(x+1)=1

X=-1,1

"x cant be negative"

Final answer: x=1

Interest

Simple Interest

I=Prt

P=principle

r=rate

t=time

I=2,000*.015*1/4

I=$2038.17

Compound Interest

A=P(1+r/n)^nt

P=principle

r=rate

n=times it compound

t=time

A=2,000(1+(0.015/4)^4*1

A=$2030.17