M.C.U.
QUE ES?
Es un movimiento de trayectoria circular en el que la velocidad angular es constante.

PARTES
PERIODO:
Es el tiempo que tarda la partícula en dar una vuelta completa. Se representa por "T" y se mide en segundos (seg)

FRECUENCIA.:
Es la cantidad de vueltas que recorre la partícula en la unidad de tiempo (1 segundo). Se representa por "f" y se mide en 1/seg ó seg

VELOCIDAD LINEAL: Es la velocidad propia de la partícula cuya magnitud es constante, pero su dirección cambia ya que siempre es tangente a la circunferencia. V = velocidad lineal
R = radio de la circunferencia
T = periodo
f = frecuencia
ω = velocidad angular

VELOCIDAD ANGULAR: Es el ángulo que se recorre en cierta cantidad de tiempo. Se representa con la letra griega ω (omega minúscula), así: ω = velocidad angular
θ = ángulo recorrido
t = tiempo
T = periodo
f = frecuencia

ACELERACIÓN:
En el MCU, la velocidad lineal permanece constante, y por lo tanto NO hay aceleración tangencial, sólo hay aceleración centrípeta. aC = aceleración centrípeta
V = velocidad lineal
R = radio de la circunferencia
T = periodo
f = frecuencia
ω = velocidad angular

FUERZA CENTRÍPETA.:
Es la fuerza necesaria para producir un Movimiento Circular Uniforme (MCU). Su dirección es perpendicular a la velocidad lineal y está dirigida hacia el centro de la circunferencia. FC = fuerza centrípeta
m = masa de la partícula
V = velocidad lineal
R = radio de la circunferencia
T = periodo
f = frecuencia
ω = velocidad angular

EJEMPLOS
EJERCICIO 1
Un móvil se desplaza con una trayectoria circular a una velocidad de 2 m/s.
¿Cuánto tardará en dar dos vueltas alrededor de una circunferencia de 100 metros de diámetro?
SOLUCIÓN
Podemos plantear el problema con las ecuaciones de velocidad tangencial (sabiendo que tiene que recorrer dos veces el perímetro) o de velocidad angular (sabiendo que tiene que recorrer dos veces el ángulo de la circunferencia completa, es decir 2π).
Dado que tenemos la velocidad tangencial vamos a plantear su ecuación y despejar el tiempo. Recordemos que la velocidad tangencial es la variación de posición respecto del tiempo.
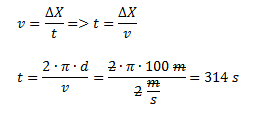
GRÁFICAS
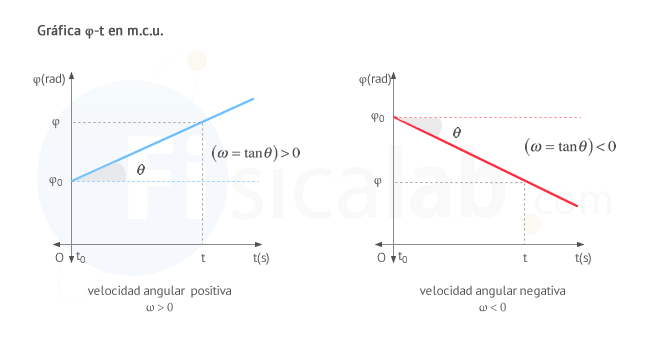
GRÁFICA POSICIÓN ANGULAR-TIEMPO:
φ=φ0+ω⋅t
representa en el eje horizontal (eje x) el tiempo y en el eje vertical la posición angular. La posición angular, φ, medida en radianes según unidades del Sistema Internacional (S.I.) aumenta (o disminuye) de manera uniforme con el paso del tiempo.
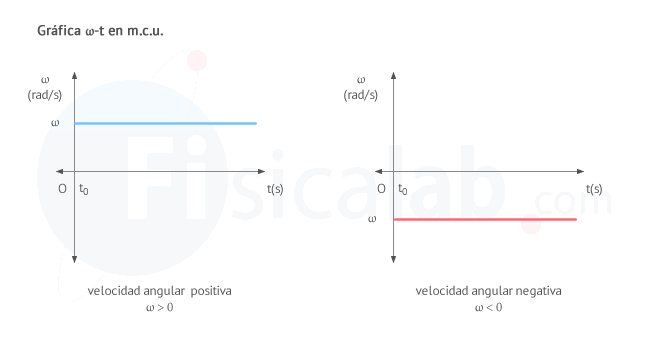
GRÁFICA VELOCIDAD ANGULAR-TIEMPO:
ω=ω0=cte
muestra que la velocidad angular ω, medida en radianes por segundo (rad/s) según el Sistema Internacional (S.I.), permanece constante a lo largo del tiempo.
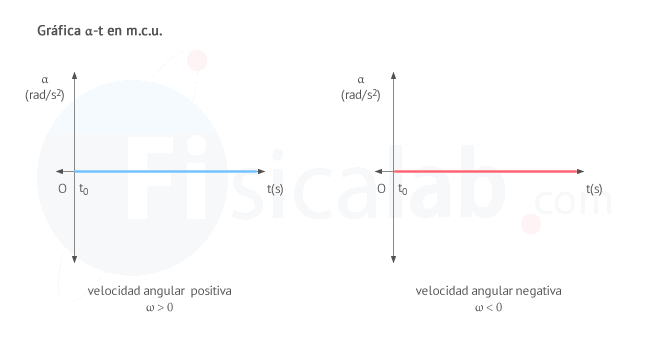
GRÁFICA ACELERACIÓN ANGULAR-TIEMPO:
α=0
muestra que la aceleración angular, medida en el Sistema Internacional (S.I.) en radianes por segundo al cuadrado (rad/s2), es nula en todo momento. En este caso, tanto si la velocidad del cuerpo se considera positiva como negativa, tenemos una sola posibilidad.