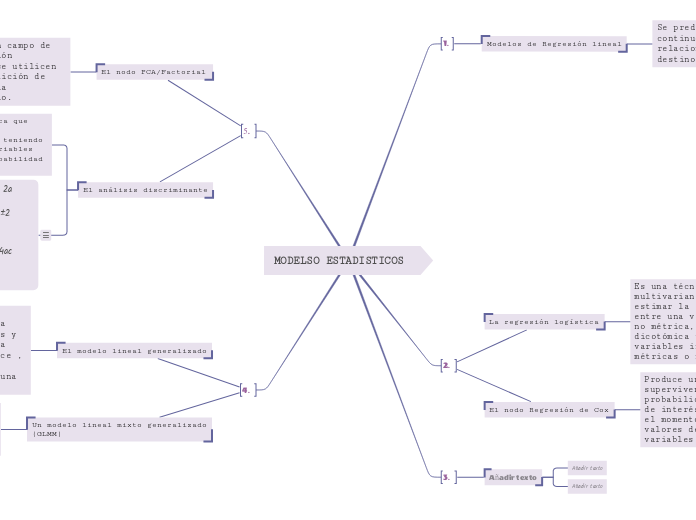
MODELSO ESTADISTICOS
Modelos de Regresión lineal
Se predicen un objetivo continuo tomando como base las relaciones lineales entre el destino y uno o más predictores
3 modelos
Lineal simple
Se trata de estudiar el efecto de una variable independiente sobre una única variable dependiente de la primera o que al menos a nivel teórico hemos considerado que es dependiente
Fórmula de la regresión lineal simple
y = B0 + B1 x + ε
Lineal múltiple
Cuenta con más de una variable independiente, este modelo lo aplicaremos cuando tengamos razones para creer que hay más de un factor que afecta a la variable de estudio.
Fórmula de la regresión lineal múltiple
Y = 0 + B1*X1 + B2*X2 + … + Bn*Xn + ε
No lineal
La relación que puede darse entre variables independientes y la variable dependiente no tenga un desarrollo lineal, sino que tengan, por ejemplo, un crecimiento exponencial.
Regresión exponencial
y = a.bx
log y = log(a.bx) = log a + x log b
La regresión logística
Es una técnica estadística multivariante que nos permite estimar la relación existente entre una variable dependiente no métrica, en particular dicotómica y un conjunto de variables independientes métricas o no métricas.
El nodo Regresión de Coxundefined
Produce una función de supervivencia que predice la probabilidad de que el evento de interés se haya producido en el momento dado (t) para valores determinados de las variables de entrada.
Añadir texto
Añadir texto
Añadir texto
El nodo PCA/Factorial
Si se ha definido un campo de partición, esta opción garantiza que sólo se utilicen los datos de la partición de entrenamiento para la generación del modelo.
El análisis discriminante
Es una técnica estadística que crea una función capaz de clasificar los fenómenos, teniendo en cuenta una serie de variables discriminadoras y una probabilidad de pertenencia.
x= 2a
−b±2
−4ac
El modelo lineal generalizado
De manera que la variable dependiente está relacionada linealmente con los factores y las covariables mediante una determinada función de enlace , el modelo permite que la variable dependiente tenga una distribución no normal.
Un modelo lineal mixto generalizado (GLMM)
Los modelos lineales mixtos generalizados cubren una amplia variedad de modelos, desde modelos de regresión lineal simple hasta modelos multinivel complejos para datos longitudinales no normales.