NOCIONES DE CONJUNTOS

Grupo o colección de objetos el cual se designa con letra mayúscula. La característica principal de un conjunto es que esté bien definido, es decir, dado un objeto particular, debe saberse con claridad si dicho objeto es o no un elemento del conjunto.

CLASES DE CONJUNTOS

IGUALES:Dos conjuntos son iguales si tienen exactamente los mismos elementos.

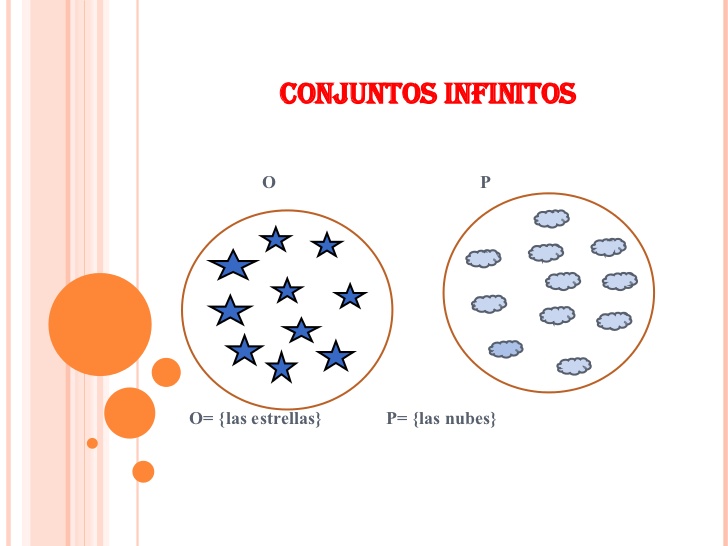
FINITOS E INFINITOS:Los conjuntos finitos, son aquellos en donde pueden ser contabilizados o enumerados todos elementos del conjunto.

SUBCONJUNTOS:Un subconjunto es una parte de un conjunto.

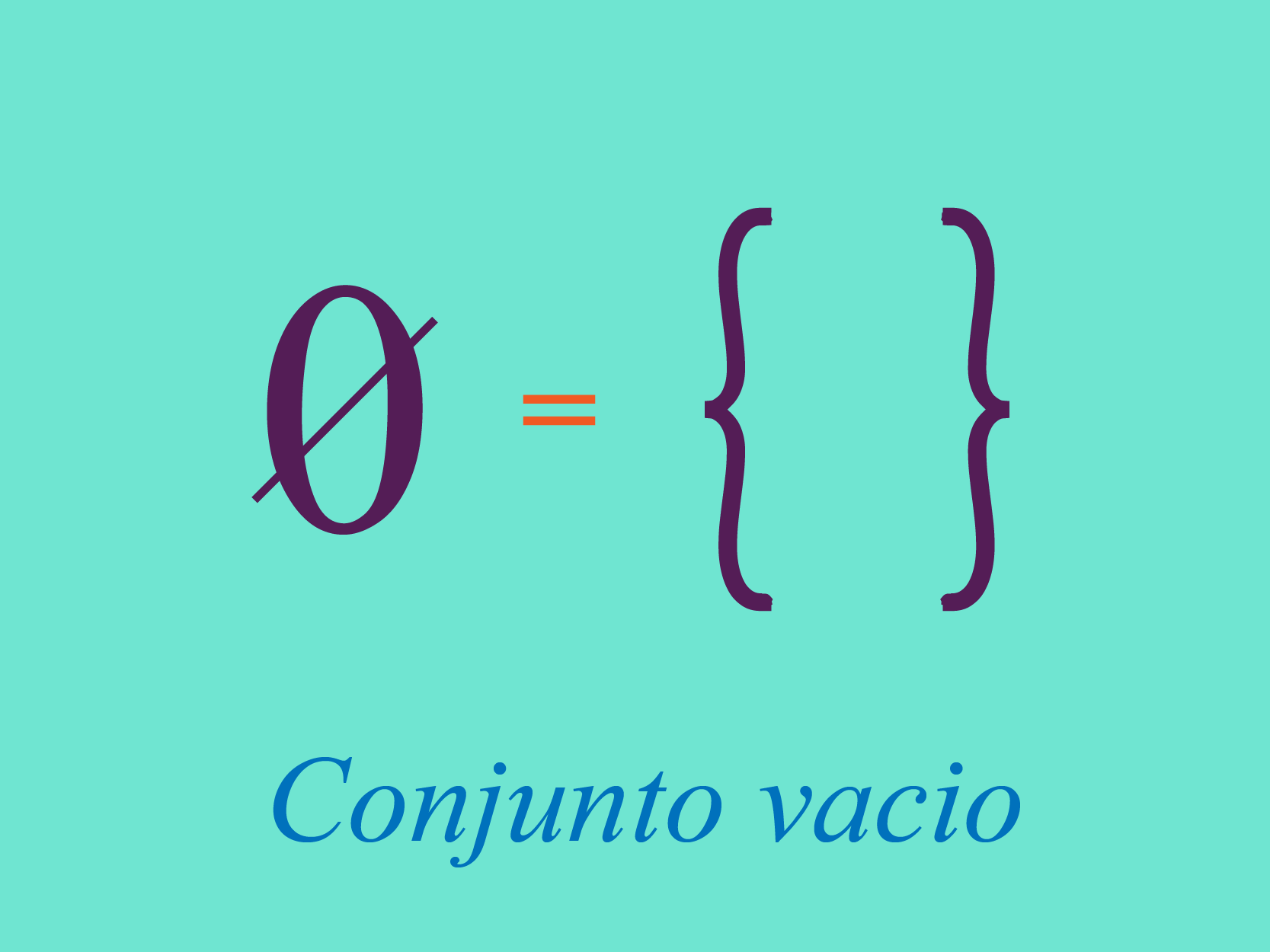
VACIO:El símbolo Ø representa el conjunto vacío, que es el conjunto que no tiene elementos en absoluto. Nada en el universo entero es un elemento de Ø.

DISJUNTOS O DISYUNTIVOS:Dos conjuntos se llaman disjuntos si no tienen elementos en común.

EQUIVALENTES:Se dice que A y B son equivalentes si tienen la misma cantidad de elementos que los constituyen, es decir, el numero cardinal del conjunto A es igual al número cardinal del conjunto B, n (A) = n (B). El símbolo para denotar un conjunto equivalente es ‘↔’.

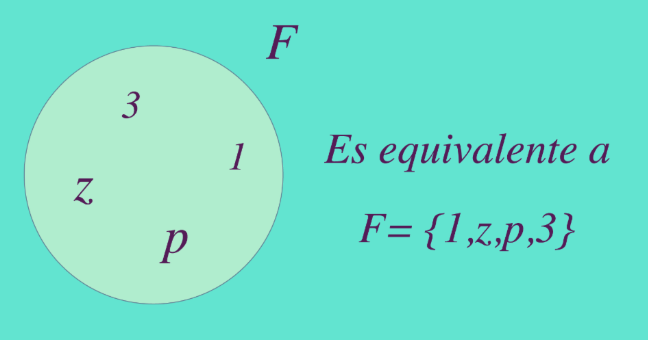
UNIVERSAL Y REFERENCIAL:Un conjunto universal es la colección de todos los objetos en un contexto particular o teoría. Todos los demás conjuntos en ese marco constituyen subconjuntos del conjunto universal, que se denomina con la letra mayúscula y cursiva U.

RELACIONES ENTRE CONJUNTOS

En el caso de la relación matemática, se trata de la correspondencia que existe entre dos conjuntos: a cada elemento del primer conjunto le corresponde al menos un elemento del segundo conjunto.

RELACIÓN DE CONSTENENCIA

Como te puedes dar cuenta, cada elemento que pertenece al conjunto pertenece también al conjunto Cuando se da esta situación decimos que un conjunto está contenido en el otro, o que es un subconjunto del otro.

RELACIÓN DE PERTENENCIA

Cuando un objeto es uno de los elementos de un conjunto decimos que pertenece al conjunto. Como has visto, es posible representar gráficamente la relación de pertenencia por medio de diagramas de Venn dibujando el elemento dentro de un circulo que representa el conjunto.