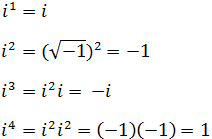Los Números Complejos
Operatorias
Conjugado
Z=a-bi
Inverso multiplicativo
Z elevado a -1
Inverso aditivo
Z =-a -bi

Ponderación
Adición
Sustracción
Multiplicación
División
Se representan como
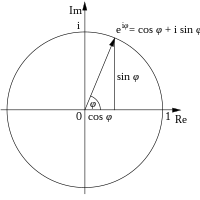
Forma trigonométrica
Donde z = lzl
(Cos arg)"2 + i (Sen arg)"2 = 1
Siendo el Seno de (arg)
Im(z): lzl
Siendo el Coseno de (arg)
Re(z): lzl
Que se puede
representar en el
plano cartesiano
Donde el ángulo formado por
el vector y el eje real se denomina
argumento

Subtema
Para arg 30°
Para arg 45°
Para arg 60°
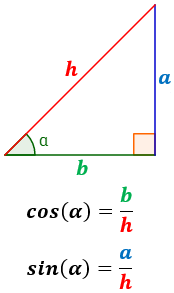
En los triangulos
rectangulos formados
por el origen y el punto
(a,b) existen las razones
Trigonometricas

Subtema
par ordenado
Se le asocia un vector
cuyo valor absoluto es
la distancia entre el
punto (a,b) y el origen
Cuyo valor corresponde
al módulo de Z
Se calcula
con Pitágoras
(a,b)
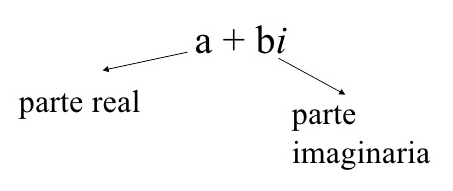
Z=a+bi
a es parte real
bi es parte imaginaria
Se clasifican
Imaginarios
Mixto
Puro
Z = 0 + bi
Reales
Z = a + 0i
Tienen Propiedades
como
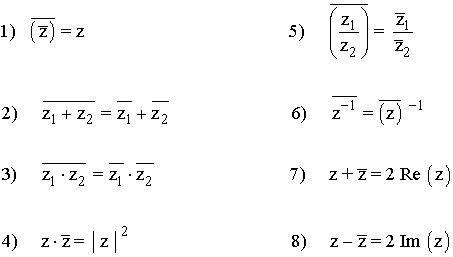
Se gráfican en un plano complejo
El eje y
Es el Imaginario
El eje x
Es el Real
Mixtos
Cuentan con la parte
imaginaria = bi
Que contiene la
Unidad imaginaria
i
con sus respectivas
potencias elevando a
1
2
3
4
La igualdad
Donde dos números complejos son
iguales solo si se cumple que
Z = W
Por lo tanto
Si (Z =a+b)
y (W =c+d)
A = C
B = D