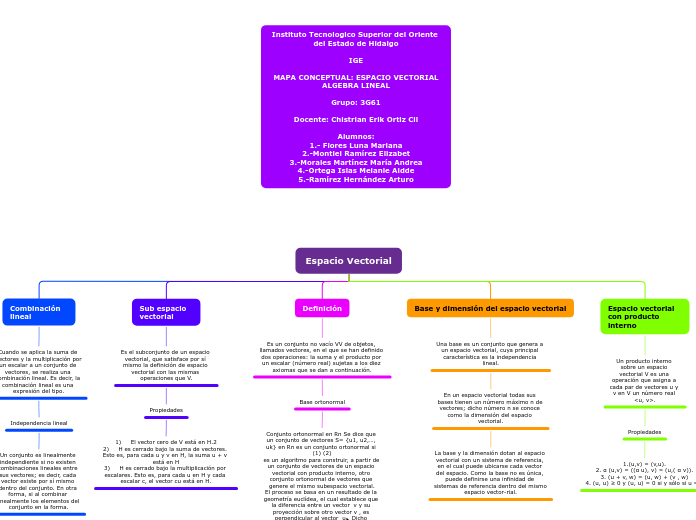
Espacio Vectorial
Combinación lineal
Cuando se aplica la suma de vectores y la multiplicación por un escalar a un conjunto de vectores, se realiza una combinación lineal. Es decir, la combinación lineal es una expresión del tipo.
Independencia lineal
Un conjunto es linealmente independiente si no existen combinaciones lineales entre sus vectores; es decir, cada vector existe por sí mismo dentro del conjunto. En otra forma, si al combinar linealmente los elementos del conjunto en la forma.
Sub espacio vectorial
Es el subconjunto de un espacio vectorial, que satisface por sí mismo la definición de espacio vectorial con las mismas operaciones que V.
Propiedades
1) El vector cero de V está en H.2
2) H es cerrado bajo la suma de vectores. Esto es, para cada u y v en H, la suma u + v está en H
3) H es cerrado bajo la multiplicación por escalares. Esto es, para cada u en H y cada escalar c, el vector cu está en H.
Definición
Es un conjunto no vacío VV de objetos, llamados vectores, en el que se han definido dos operaciones: la suma y el producto por un escalar (número real) sujetas a los diez axiomas que se dan a continuación.
Base ortonormal
Conjunto ortonormal en Rn Se dice que un conjunto de vectores S= {u1, u2,…, uk} en Rn es un conjunto ortonormal si (1) (2)
es un algoritmo para construir, a partir de un conjunto de vectores de un espacio vectorial con producto interno, otro conjunto ortonormal de vectores que genere el mismo subespacio vectorial.
El proceso se basa en un resultado de la geometría euclídea, el cual establece que la diferencia entre un vector v y su proyección sobre otro vector v , es perpendicular al vector u₁. Dicho resultado constituye una herramienta para construir, a partir de un conjunto de dos vectores no paralelos, otro conjunto, conformado por dos vectores perpendiculares.
IMPORTANCIA DEL TEMA
Es importante este tema ya que nos da a conocer como el espacio vectorial tiene relación con otras areas de las matematicas y como se aplica en las mismas
Base y dimensión del espacio vectorial
Una base es un conjunto que genera a un espacio vectorial, cuya principal característica es la independencia lineal.
En un espacio vectorial todas sus bases tienen un número máximo n de vectores; dicho número n se conoce como la dimensión del espacio vectorial.
La base y la dimensión dotan al espacio vectorial con un sistema de referencia, en el cual puede ubicarse cada vector del espacio. Como la base no es única, puede definirse una infinidad de sistemas de referencia dentro del mismo espacio vector-rial.
Espacio vectorial con producto interno
Un producto interno sobre un espacio vectorial V es una operación que asigna a cada par de vectores u y v en V un número real <u, v>.
Propiedades
1.(u,v) = (v,u).
2. α (u,v) = ((α u), v) = (u,( α v)).
3. (u + v, w) = (u, w) + (v , w)
4. (u, u) ≥ 0 y (u, u) = 0 si y sólo si u = 0