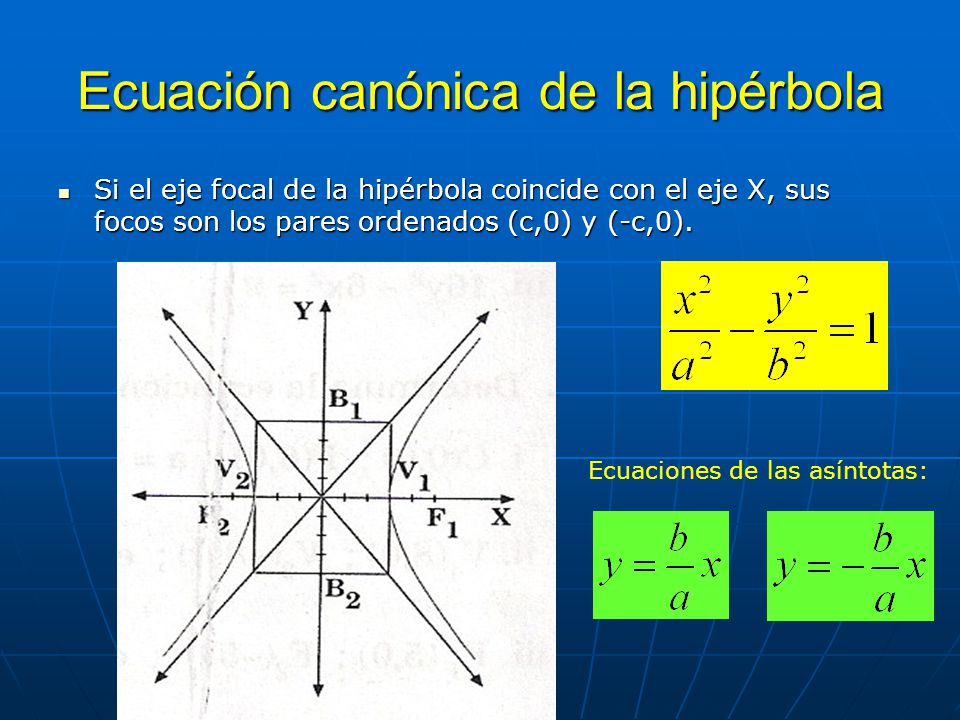
sexione conicas
q son las sxciones conicas?Una sección cónica es la intersección de un plano y un cono. Cambiando el ángulo y el lugar de la interseccón, podemos crear un círculo, un elipse, una parábola o una hipérbola; o en el caso especial cuando el plano se pone en contacto con el vértice: un punto, una línea o 2 líneas intersectadas.

se dibide en
hiperbola
circunferencia
parabola
elpse

Resultados de la búsqueda
Resultado de imagen de q es parabola matematica
Se denomina parábola al lugar geométrico de los puntos de un plano que equidistan de una recta dada, llamada directriz, y de un punto exterior a ella, llamado foco
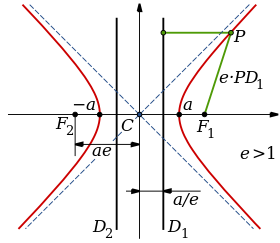
Resultado de imagen de que es hiperbola matematicas
Una hipérbola (del griego ὑπερβολή) es una sección cónica, una curva abierta de dos ramas obtenida cortando un cono recto por un plano oblicuo al eje de simetría, y con ángulo menor que el de la generatriz respecto del eje de revolución.
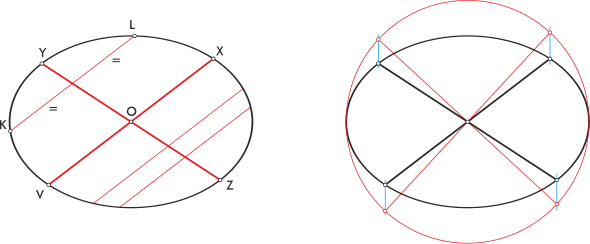
La elipse es el lugar geométrico de todos los puntos de un plano, tales que la suma de las distancias a otros dos puntos fijos llamados focos es constante.

La circunferencia es una curva plana y cerrada donde todos sus puntos están a igual distancia del centro. Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan de otro punto fijo y coplanario llamado centro en una cantidad constante que se denomina radio.
caracteristicas
caracteristicas
ecuaasion canonica
caracteristicas


caracteristicas


ecuacion canonica
ecuacion general

Ecuación de la parábola en la forma general
Aceptamos el significado de general como la parábola cuyo vértice no está situado en el origen de coordenada
Supongamos que el vértice de una parábola cuando su eje focal es paralelo al eje Y se halla situado en el punto (h,k).
En este caso tendremos que trasladar el vértice al nuevo punto quedándonos establecida la fórmula:
Ecuación canónica de la parábola con vértice en (h.k) Si p < 0, la parábola abre hacia la izquierda. La ecuación canónica de la parábola con vértice en (h,k) y eje de simetría paralelo al eje x es: (y-k)² = 4p(x-h). donde p es la distancia que el vértice al foco.
ecuacion general