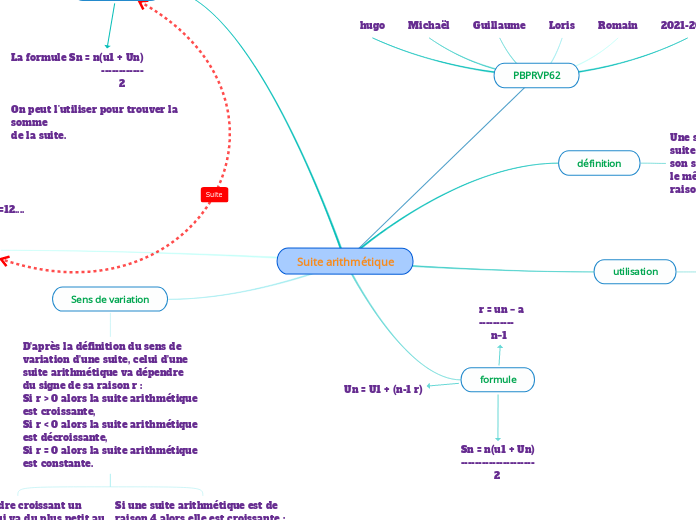
Suite arithmétique
définition
Une suite arithmétique est une suite où l’on passe d’un terme à son suivant en ajoutant toujours le même nombre r appelé la raison.
utilisation
Les scientifiques utilise les suites arithmétiques
formule
r = un − a
----------
n−1
Un = U1 + (n-1 r)
Sn = n(u1 + Un)
---------------------
2
application
La formule r = un − a
----------
n−1
On peut l'utiliser pour trouver la raison de la suite .
La formule Un = U1 + (n-1 r)
On peut l'utiliser pour trouver le terme de la
suite .
La formule Sn = n(u1 + Un)
------------
2
On peut l'utiliser pour trouver la somme
de la suite.
exemple
Un=6 r=2
6+2=8+2=10+2=12....
Un=3n-2.
Un+1 – Un= 3(n+1)-2-(3n-2)= 3n+3-2-3n+2 = 3 donc (Un) est une suite arithmétique de raison 3.
U10 = U0+ 10×r = -2 + 10×3 = 28.
S10 = 11 × (-2 + 28)/2 = 11 × 26/2 = 11 × 13 = 143.
Sens de variation
D’après la définition du sens de variation d’une suite, celui d’une suite arithmétique va dépendre du signe de sa raison r :
Si r > 0 alors la suite arithmétique est croissante,
Si r < 0 alors la suite arithmétique est décroissante,
Si r = 0 alors la suite arithmétique est constante.
On appelle ordre croissant un classement qui va du plus petit au plus grand. Inversement, l'ordre décroissant va du plus grand au plus petit. On peut classer des nombres par ordre croissant ou par ordre décroissant. Le plus grand nombre est du côté ouvert du signe et le plus petit nombre du côté fermé.
Si une suite arithmétique est de raison 4 alors elle est croissante :
U0 = 1 ; U1 = 5 ; U2 = 9 ; U3 = 13…
Si une suite arithmétique est de raison -5 alors elle est décroissante :
U0 = 4 ; U1 = − 1 ; U2 = − 6 ; U3 = − 11…