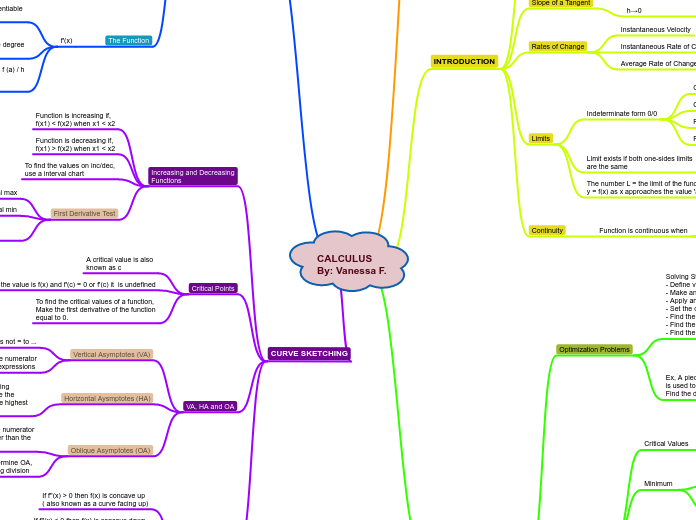
CALCULUS By: Vanessa F.

MATH 1512-70

by Jackie Lindquist

The Six Trigonometric Functions

by Kendrick Williams ll

VM266 0847

by Rico Tan

Unit 4 Equations

by María Pardo

CURVE SKETCHING

Concavity/ P.O.I

Second Derivative Test

If f'(c) and f''(c) < 0, then local max at c

If f'(c) + 0 and f''(c) > 0, then local min a c

The Point of Inflection is defined if f''(x) changes sign at x.

If f''(x) < 0 then f(x) is concave down ( also known as a curve facing down)

If f''(x) > 0 then f(x) is concave up ( also known as a curve facing up)

VA, HA and OA

Oblique Asymptotes (OA)

To determine OA, use long division

If the degree on the numerator is one degree higher than the denominator

Horizontal Aysmptotes (HA)

To determine limits as x approaching infinity of a rational function, divide the numerator and denominator by the highest degree then simplify

Vertical Asymptotes (VA)

Is determined by factoring the numerator and denominator of rational expressions

Domain restriction is, x is not = to ...

Critical Points

To find the critical values of a function, Make the first derivative of the function equal to 0.

if the value is f(x) and f'(c) = 0 or f'(c) it is undefined

A critical value is also known as c

Increasing and Decreasing Functions

First Derivative Test

If f'(x) sign does not change then the max and min D.N.E at c

If f'(x) changes from - to +, f has a local min

If f'(x) changes from + to - , f has a local max

To find the values on inc/dec, use a interval chart

Function is decreasing if, f(x1) > f(x2) when x1 < x2

Function is increasing if, f(x1) < f(x2) when x1 < x2

FIRST DERIVATIVES

The Function

f'(x)

f'(x) = lim f ( a + h ) - f (a) / h h→0

f'(x) is always one degree less than f(x)

Function f(x) is differentiable only if f'(a) exists

Its not differentiable if f(x) is - Cusp - Vertical Tangent - Discontinuity - Corner

Polynomial Functions

Horizontal Tanget

When the slope of a tangent is at 0

Constant Function Rule

f(x) = k, then f'(x) = 0

Power Rule

f(x) =x^n, then f'(x) = nx^n-1

Constant Multiple Rule

f(x) = k [g(x)], then f'(x) = K [g'(x)]

Sum and Differences Rule

f(x) = p(x) +- q(x), then f'(x) = p'(x) +- q'(x)

Lebniz Notation

y' = dy/dx

f(x) = f'(x)

Product Rule

Power of a Function Rule

f'(x) = n[g(x)] ^n-1 . g'(x)

f'(x) = p'(x) . q(x) + p(x) . q'(x)

Quotient Rule

f'(x) = p'(x) . q(x) - p(x) . q'(x)/ [q(x)]^2

Composite Functions

Chain Rule

h'(x)= f'(g(x)) . g'(x)

Lebniz Notation dy/dx = dy/du - du/dx

Defined as (f. g) = f(g(x))

SECOND DERIVATIVES

Velocity and Acceleration

Acceleration

This is known as the second derivative of the s(t) and first derivative of v(t)

The instantaneous rate of change of the velocity with respect to time

a(t) = v'(t) = s''(t)

Velocity

-If the object is moving up or right, the v(t) is > 0 -If the object is moving down or left, the v(t) is < 0 - If the object is at rest, v(t) = 0

The instantaneous rate of change of the position function s(t)

v(t) = s'(t)

The function notation for the second derivative is considered as, f''(x)

To find the second derivative, You have to find the first derivative of the function being given.

ex, f(x) = 2x^2 + 5x + 6 f(x) = 4x + 5 f''(x) = 4 Therefore, the second derivative is 4.

Extreme Values

To find the max and min on an interval: - Differentiate - Set f'(x) = 0 - Solve of x in f'(x) = 0 or where f'(x) D.N.E - Test values - Compare the tested values

Maximum

Absolute max - the highest point on a graph

Local max - the second highest point on a graph

Minimum

Absolute min - the highest point on the graph

Local min - the second lowest point on a graph

Critical Values

f'(c) = 0 or f'(c) D.N.E

Optimization Problems

Ex, A piece of cardboard, 80 cm by 40 cm, is used to make an open-top rectangular box. Find the dimensions for the box with the largest volume.

First I would draw a diagram to better understand the question. Then I would let x represent the width of the removed square. For this particular question, I would use the formula V = (L)(W)(h) I then plug the number given in the question into this formula and find the first derivative. I ten set the derivative to 0. Once i find the critical value, I find my test values and the dimensions.

Solving Steps: - Define variables - Make an equation that defines the question - Apply any substitutions if needed - Set the derivative to 0 - Find the critical values - Find the test values - Find the domain and range

INTRODUCTION

Continuity

Function is continuous when

f(a) is defined

both side limits are equal

limit of f(x) = f(a)

Limits

The number L = the limit of the function y = f(x) as x approaches the value 'a'

Limit exists if both one-sides limits are the same

Limit D.N.E if the one-sides limits are not the same

Indeterminate form 0/0

FACTORING if there is a restriction

RATIONALISING if there is a square root

CHANGE OF VARIABLE if there a cube roots or other

ONE SIDED LIMITS if it is a absolute value

Rates of Change

Average Rate of Change

< Slope of the secant

Instantaneous Rate of Change

< Slope of the tangent

Instantaneous Velocity

Slope of a Tangent

lim f ( a + h ) - f (a) / h h→0

lim f ( a + h ) - f (a) / h

h→0

Radical Expressions

√a x √a = √a2 = a (a - b) (a+b) = a2 - b2 ( √m - √n ) ( √m + √n ) = √m2 - √n2 = m - n

√a x √a = √a² = a

(a - b) (a+b) = a² - b²

( √m - √n ) ( √m + √n ) = √m² - √n²= m - n

when there is no denominator, simplify.

MINOMIAL

If the expression is in the denominator, rationalise by multiplying the numerator and denominator by its conjugate.

If the expression is the numerator, rationalise by multiplying the numerator and denominator by its conjugate.

EXPONENTIAL & TRIGONOMETRIC WITH DERIVATIVES

Trigonometric

If f(x) = tan x then f'(x) = sec^2 x

also, tanx = sinx/cosx

ex, y= (sinx + tan x)^4 dy/dx= 4 (sinx + tanx)^3 . (cos + sec^2x) = 4 ( cosx + sec^2 x ) ( sinx + tanx)^3

CALCULUS By: Vanessa F.

MATH 1512-70

The Six Trigonometric Functions

VM266 0847

Unit 4 Equations