Al anticipar el desarrollo de la clase y prever las condiciones necesarias para
que ocurran las interacciones que nos interesan, diseñamos una situación problemática a propósito del conocimiento que queremos enseñar. Esta situación incluye un conjunto de elementos y relaciones que estarán presentes en la
clase: el problema, los materiales, una cierta organización del grupo, un desarrollo con momentos para diferentes intercambios.
Para que los alumnos desarrollen el tipo de trabajo
matemático que se busca promover, serán fundamentales las intervenciones
del docente durante la clase.
Para lo cual es necesario la gestión de la clase:
Para iniciar el aprendizaje de un nuevo conocimiento, es necesario presentar un problema asegurase de que todos hayan comprendido. cual es, el desafío que se le propone para que cada alumno acepté ocuparse de el, es esencial generar el deseo de resolverlo. Es una invitación para que el chico resuelva por si solo y no una orientación sobre como debe hacerlo.
Los niños lo resuelvan manera individual o grupal, con diferentes procedimientos, según los conocimientos previos que disponga cada uno.
A su vez:
Es necesario anticipar cuál es el tipo de interacciones que queremos que se den para organizar distintos momentos de la clase: las de los alumnos con el maestro, de los alumnos entre sí, y entre cada alumno y el problema.
Para lo cual es necesario tener en cuenta el tratamiento de las informaciones.
Una manera de modificar esta cuestión es generar en los chicos la necesidad de leer e interpretar el enunciado del problema y, por lo tanto, de construir una representación mental que les permita encontrar algún procedimiento de resolución. Para ello, será necesario variar tanto la forma de presentación del enunciado como el tipo de tarea que el alumno debe realizar.
Muchas veces se detecta que los alumnos intentan resolver el problema que sin pensar el enunciado, buscando sólo qué operación deben realizar para solucionarlo. Aunque con frecuencia esa forma de resolver problemas es fomentada por los mismos enunciados que forman parte de la tradición escolar y por el tratamiento que se les da en clase. Suelen aparecer todos los datos necesarios para responder la pregunta que se hace.
CONTEXTO MATEMÁTICO: hace referencia a lo matematico
CONTEXTO NO MATEMATICO: incluyendo entre estos últimos los de la vida cotidiana, los ligados a la información que aparece en los medios de comunicación y los de otras disciplinas.
Tipos de contextos:
Es posible considerar diferentes contextos que nos permitan plantear problemas en los que la resolución requiera su uso.
Una noción matemática cobra sentido a partir del conjunto de problemas en los cuales resulta un instrumento eficaz de resolución.Esos problemas constituyen el o los contextos para presentar la noción a los
alumnos.
Es necesario tener en
cuenta las distintas representaciones posibles de la noción que se quiere enseñar, ya que la posibilidad de avanzar en la comprensión de una noción implica
reconocerla en sus distintas representaciones pudiendo elegir la más conveniente y pasar de una a otra en función del problema a resolver.
Es donde por medio de una actividad, en los alumnos resulta un enigma, un desafío a sus conocimientos matemáticos, es decir, si estos le permiten iniciar la resolución del problema y, para hacerlo, elabora un cierto procedimiento y pone en juego las nociones que tiene disponibles, modificándolas y estableciendo nuevas relaciones.
Problemas matemáticos
Se puede generar un conocimiento a través de:
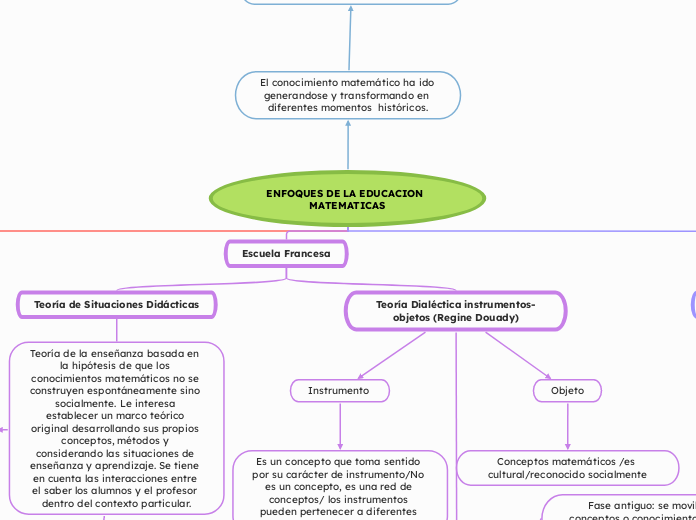
El conocimiento matemático ha ido generandose y transformando en diferentes momentos históricos.
Situación a didáctica: cuando el alumno y el docente logran que el primero asuma el problema planteado como propio y entra en un proceso de búsqueda autónoma sin ser guiado,lo que el profesor espera.
fase del proceso en la cual se da el aprendizaje y no la enseñanza, el alumno no puede resolver de entrada cualquier situación a didactica y por esta razón el docente la acondiciona para que esté a su alcance,el docente comunica o se abstiene de comunicar según el caso informaciones, preguntas, etc a partir de ese momento y hasta que produce su respuesta el docente no interviene en la puesta en escena de los conocimientos que el alumno debe construir.
Situación didáctica:un conjunto de relaciones establecidas explícita o implícitamente, entre un alumno o un grupo de alumnos, un cierto medio, (que comprende eventualmente instrumentos u objetos) y un sistema educativo, (profesor) con la finalidad de lograr que estos alumnos se apropien de un saber constituido o en vías de construcción.
ENFOQUES DE LA EDUCACION MATEMATICAS
Escuela Anglosajona
Resolución De Problemas
El foco esta puesto que el estudiante aprenda a resolver problemas. el docente no va a proponer un contenido conceptual a enseñar sino que su interés va a estar que el estudiante se desenvuelva aprenda resolver problemas, adquieras estrategias para encarar ese resolución de problema. que reconocer su accionar cognitivo, que sea consiente de lo que esta haciendo al momento de abordar el problemas.
Concepto de problemas- concepto problema para un sujeto" diversidades de definiciones lo que comparten: la preseencia de alguien que resuelva, relativamente al sujeto ( lo que es problema para uno, para otro no es problema), una meta por logar, un bloqueo o resistencia inicial.
Metacognicion:
Reflexiona sobre su propia cognición. antes los bloqueos los estudiantes reconocen sus procedimientos permitiéndoles accionar de una manera u otras, utilizando distintas estrategias.
Heurísticas
Estrategias utilizadas en el proceso de resolución de problemas/ se pone en juego cuando el sujeto esta enfrentado a la tarea de resolver un problema.
Escuela Francesa
Teoría Dialéctica instrumentos-objetos (Regine Douady)
Objeto
Conceptos matemáticos /es cultural/reconocido socialmente
Fases de análisis
Fase de Familiarización- reinversión: Se reutiliza el concepto en diferentes situaciones.
Fase de Institucionalización: el docente presenta en forma organizada y clara los conceptos.
Fase de Explicación: se comunica la resolución o conclusión del problema.
Fase de busqueda: el alumno encuentra dificultades para resolver un problema, puede encontrar dificultades como su procedimientos es muy costoso, tambien que la estrategia no sirva.
Fase antiguo: se movilizan conceptos o conocimiento previos en forma total o parcial.
Instrumento
Es un concepto que toma sentido por su carácter de instrumento/No es un concepto, es una red de conceptos/ los instrumentos pueden pertenecer a diferentes marcos.
Teoría de Situaciones Didácticas
Teoría de la enseñanza basada en la hipótesis de que los conocimientos matemáticos no se construyen espontáneamente sino socialmente. Le interesa establecer un marco teórico original desarrollando sus propios conceptos, métodos y considerando las situaciones de enseñanza y aprendizaje. Se tiene en cuenta las interacciones entre el saber los alumnos y el profesor dentro del contexto particular.
Conceptos Importantes
Se presentas varios tipos de situaciones:
Institucionalización: Se saca conclusiones a partir de lo producido por los alumnos. se debe vincular para establecer relaciones entre las producciones de los alumnos y el saber cultural.
Situacion de Validacion: se trata de convencer a uno o varios interlocutores de la valides delas afirmaciones que hacen.
Situación Formulación: requiere la comunicacion del estudiante, la modificacion del lenguaje que utiliza habitualmente, precisándolo y adecuandolo a las informaciones que debe comunicar. comparten experiencias en la construcción del conocimientos .
Situación de acción: El estudiante trabaja con el problema, aplica conocimientos previos y desarrolla un determinado saber, interactuando con el medio didactico.
Medio: el objeto de interacción de los alumnos, es la tarea específica que deben llevar a cabo y las condiciones en que deben realizarla,es decir el ejercicio/ problemas
incluye también las acciones del maestro, la consigna que da, las restricciones, informaciones y las ayudas que proporciona, expectativas que se tiene sobre la acción de los alumnos.
El autor expresa que el alumno aprende al adaptarse al medio que es factor de contradicciones, desequilibrio.el aprendizaje es la adaptación del alumno al medio del cual se retroalimenta, implica necesariamente rupturas, en esta instancia aparecen los obstáculos que brousseau los de define como un conocimiento que ha sido eficiente para resolver algún tipo de problema, pero que falla cuando se aplica a otro,debido a su éxito previo se resiste a ser modificado, rechazado.
Enfoques Cognitivista
Elementos de análisis
Representaciones
Duval: Enseñar y aprender matemática conlleva actividades cognitivas que requieren del lenguaje natural o de las imágenes, el uso de distintos registros de representación y de expresión.
un sistema semiótico puede ser un registro de representación, si permite tres actividades cognitivas relacionadas con la semiósis:
1) La presencia de una representación identificable.
2)El tratamiento de una representación que es la transformación de la representación dentro del mismo registro donde ha sido formulada..
3) La conversión es la transformación de la representación en otra representación de otro registro en la que se conserva la totalidad o parte del significado de la representación inicial
Los registros de representaciónes usuales
-numerico
-simbolico
-grafico
-verbal
Teoría de Campos Conceptuales (Vergnaud)
Es un conjunto de problemas o situaciones cuyo tratamientos requiere de conceptos, procedimientos y representaciones de tipos diferentes pero íntimamente relacionadas.
Son construcciones que hacen los niños a lo largo de varios años. el concepto adquiere sentido a través de situaciones y/o problemas que los niños pretenda resolver.
Tipos de Situaciones
Aquellas para las que el sujeto dispone de competencias necesarias para el tratamiento relativamente inmediato de la situación.
Aquella para las que el sujeto no tiene todas las competencias necesarias. lo cual lo obliga a reflexionar y a explorar en sus esquemas de representación.
Esquemas: organización invariable de la acción del sujeto para una clase situaciones especificas.
Los conocimientos contenidos en los esquemas se denominan Invariantes Operatorios
hay dos tipos
Teoremas-en -acción: propiedades usadas por los alumnos que pueden ser falsas o no.
Conceptos -en -accion/ construido pragmáticamente por los alumnos