Distribuciones de Probabilidad Variable Discreta Y Modelos Distribución de Probabilidad Variable Discreta
Distribución Binominal
Hay dos resultados posibles en cada ensayo de un experimento.


n = número de ensayos
p = probabilidad de éxito en cada ensayo
q = (1-p) = probabilidad de fracaso
x = número de éxitos en n ensayos
Caracterisitcas
a) Debe existir un número fijo de pruebas
b) Cada una de las n pruebas debe tener dos resultados, favorable o desfavorable, por
lo tanto son sucesos mutuamente excluyentes.
c) La probabilidad de éxito de un acontecimiento es fijo, igual sucede con la
probabilidad de fracaso.
d) Las pruebas son independientes, ya que el resultado de un ensayo no afecta el
resultado de otro.
e) Nos interesa el número de éxitos en n pruebas
Distribución de Poisson

λ = np
e = La base de los logaritmos naturales
x = Número de éxitos
Para considerar que nos encontramos en un evento raro (n grande y p cercana a 0) el valor
de n debe ser mayor de 50 λ debe ser menor a 5 (λ<5).
Variable aleatoria
función de valor real que tiene como dominio el espacio muestral asociado
a un experimento
Las variables aleatorias generalmente se denotan por las letras X, Y, Z.
Variable aleatoria discreta
Solo puede tomar algunos valores entre dos números
dados.
(Valores enteros)
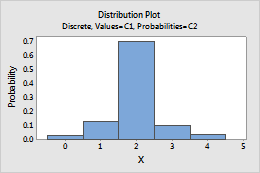
Distribución de probabilidad de una variable aleatoria discreta
Es una tabla, gráfica o fórmula que se usa para especificar todos los valores posibles de la variable, junto con sus respectivas probabilidades.
1. P(Xi) ≥ 0
2. ∑ P(Xi) = 1

Valor esperado o Media
Propiedades
1. E[c] = c, donde c es una constante
2. E[cX] = cE[X]
3. E[X+c] = E[X] + c
4. E[X+Y]=E[X] + E[Y], donde X y Y son variables aleatorias
5. E[aX+bY] = aE[X] + bE[Y], donde a y b son constantes y X y Y son variables aleatorias
Varianza
Propiedades
1. V[X] ≥ 0
2. Si c es una constante V[X] = 0
3. V[cX] = c^ 2 V[X], donde c es una constante y X una variable aleatoria
4. V[X+c] = V[X], donde c es una constante y X una variable aleatoria
5. V[X] = E[X^2] – (E[X])^2