Энтропия
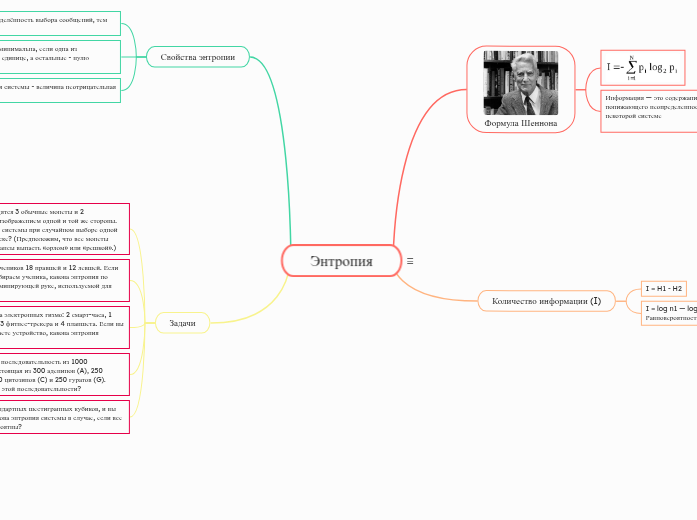
Формула Шеннона
Информация — это содержание сообщения, понижающего неопределенность наших знаний о некоторой системе
Количество информации (I)
I = H1 - H2
I = log n1 — log n2 = log (n1/n2)
Равновероятностные сообщения
Свойства энтропии
Чем больше неопределённость выбора сообщений, тем больше энтропия.
Неопределённость минимальна, если одна из вероятностей равна единице, а остальные - нулю
Энтропия системы - величина неотрицательная
Задачи
В коробке находятся 3 обычные монеты и 2 двусторонние с изображением одной и той же стороны. Какова энтропия системы при случайном выборе одной монеты и её броске? (Предположим, что все монеты имеют равные шансы выпасть «орлом» или «решкой».)
В классе из 30 учеников 18 правшей и 12 левшей. Если мы случайно выбираем ученика, какова энтропия по отношению к доминирующей руке, используемой для написания?
У вас есть 4 типа электронных гизмо: 2 смарт-часа, 1 умный телефон, 3 фитнес-трекера и 4 планшета. Если вы случайно выбираете устройство, какова энтропия выбора?
Пусть у вас есть последовательность из 1000 нуклеотидов, состоящая из 300 аденинов (A), 250 тиминов (T), 200 цитозинов (C) и 250 гуратов (G). Какова энтропия этой последовательности?
У вас есть 5 стандартных шестигранных кубиков, и вы бросаете их. Какова энтропия системы в случае, если все исходы равновероятны?