FIELDS

Gravitational Fields
What Are Gravitational Fields?
A gravitational field is a region around any body with mass in which other bodies with mass will be attracted to the object.
Gravitational field lines always point towards the center of the object.
Newton's Law of Universal Gravitation
Newton's law of universal gravitation states that the force of attraction between any two bodies with mass is directly proportional to the masses of the bodies and inversely proportional to the square of the distance between their centers.

The formula for the law of universal gravitation is:
Fg = Gm1m2/r2
Here:
- G is the gravitational constant, equal to 6.67 * 10-11 Nm2/kg2
- m1 and m2 are the masses of the two bodies
- r is the distance between their centers
Orbital Velocity
Suppose we have an object with mass m orbits a planet with mass M at a distance r from its center, in a perfectly circular path. We want to find its orbital velocity v.
Here, the gravitational force provides the centripetal force, so we equate the two:
mv2/r = GMm/r2
v2 = GM/r
v = √(GM/r)
Gravitational Field Strength
Suppose we have an object with mass m located at a distance r from the center of a planet with mass M. We want to find the gravitational field strength g (in other words, the acceleration due to gravity).
Here, we equate the gravitational force to the weight of m:
mg = GMm/r2
g = GM/r2
From this, we know that gravitational field strength follows an inverse-square relationship. This means, for example, doubling distance reduces g by 4x, tripling it by 9x, etc.
Applications of Gravitational Fields
Rocket Launches

When launching a rocket, scientists must analyze its interactions with Earth's gravitational pull in order to determine its trajectory.
Satellites
When placing a satellite into orbit, scientists must ensure it has enough speed to orbit Earth at any given distance.
For geostationary orbits (24h orbital period), the satellite must orbit at a very specific altitude above Earth's surface.
Astrophysics
/https://tf-cmsv2-smithsonianmag-media.s3.amazonaws.com/filer/fe/67/fe6786cc-be25-4fca-b638-1856f3b02520/do7hr.jpg)
The analysis of the gravitational fields of massive bodies (e.g., stars, black holes) is essential for understanding the behaviors of these objects.
Electric Fields
What Are Electric Fields?
An electric field is a region around any charged particle or object in which other charged particles or objects would experience a force.
Charges with like signs repel one another, and charges with opposite signs attract one another.
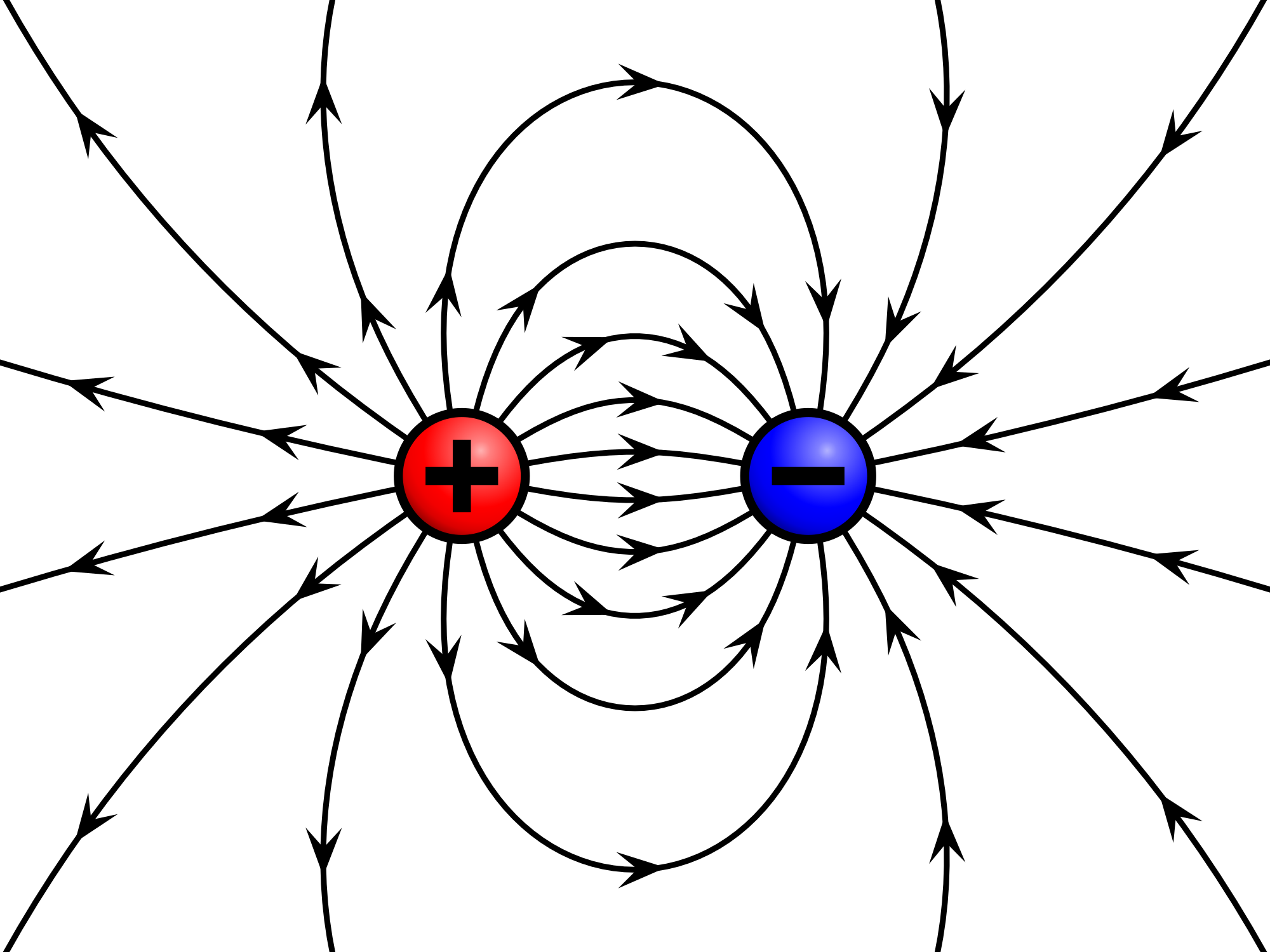
Electric field lines always point away from positive charges and towards negative charges.

Electric field strength (E) is represented by the electric force exerted by the field per unit of charge. Thus, the units of electric field strength are N/C.
This formula also takes the sign of the charge into account, which means that positive charges accelerate along the electric field while negative charges accelerate against the electric field.
Coulomb's Law
Coulomb's law states that the electric force between any two charged particles is directly proportional to the magnitude of the charges and inversely proportional to the square of the distance between the charges.

The formula for Coulomb's law is:
Fe = kq1q2/r2
Here:
- k is Coulomb's constant, equal to 9.0 * 109 Nm2/C2
- q1 and q2 are the charges of the two particles
- r is the distance between their centers.
The signs of the charges are taken into account.
Subtopic
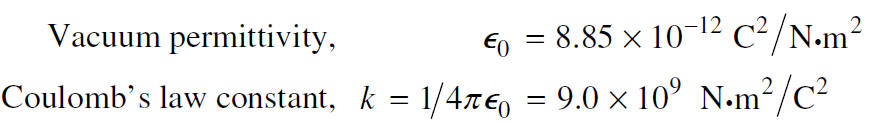
Note also that k = 1/(4πε0), where ε0 is vacuum permittivity. The permittivity of a material refers to its ability to store electrical energy within an electric field. ε0 = 8.854 * 10-12 C2/N.
Coulomb's law explains helps explain why like charges repel while opposite charges attract.
Suppose we have two charges, q1 and q2, with q2 being on the right. From q1's reference frame, we define right as the "positive" direction. From q2's reference frame, we define left as the "positive" direction.
This is because, for example, when q1 pushes q2 away, q2 moves right.
Electric Field Strength
Suppose we have a positive test charge q, and we have a source charge Q. The test charge is positive by convention. We want to find Q's electric field strength E at a distance r.
Here, we equate our two different formulas for electric force:
kQq/r2 = qE
E=kQ/r2
From this, we know that electric field strength, just like gravitational field strength, follows an inverse-square relationship.
Electric Field Lines

By convention, electric field lines always point away from positive charges and towards negative charges.
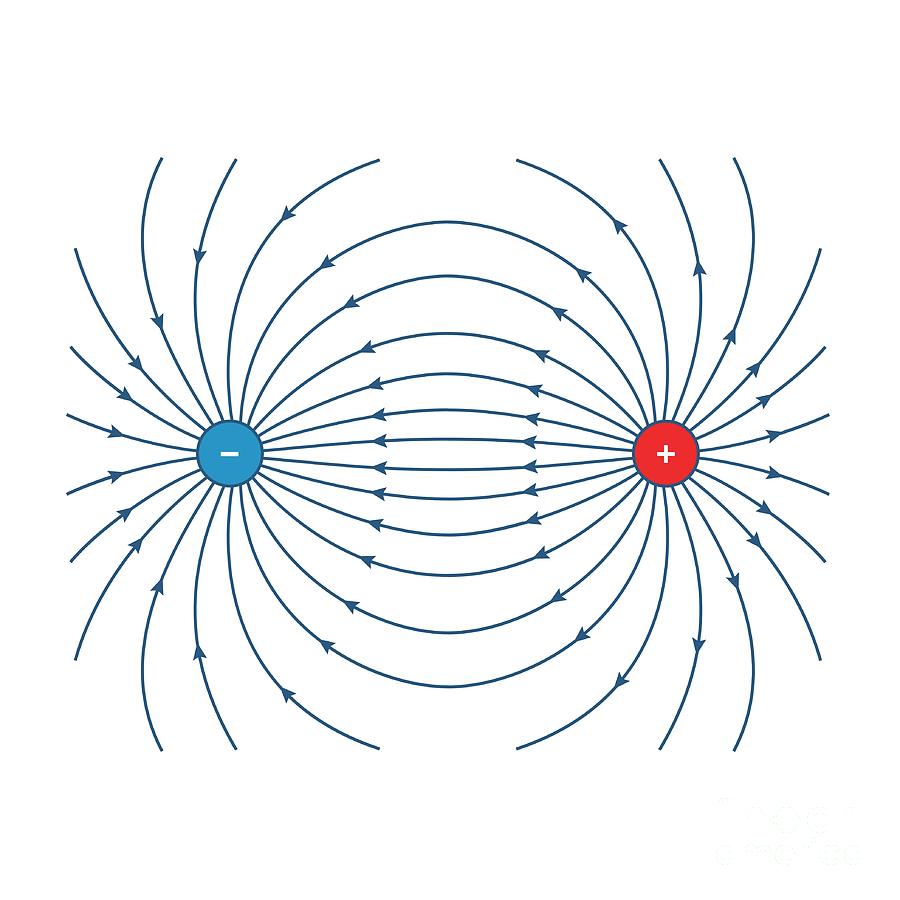
If two opposite charges are placed together, the electric field lines travel from the positive charge to the negative charge and curve outwards in order to avoid touching one another.
This results in what is known as an electric dipole.

If two like charges are placed together, their electric field lines behave in such a way that they behave like one charge.
Increasing the magnitude of any charge results in greater curvature of electric field lines around that charge.
In the case of two parallel, equally but oppositely charged plates, the electric field is uniform between the plates and is curved at the edges. The field points from the positive plate to the negative plate.
Electric Potential, Voltage, and Electric Potential Energy
Electric Potential
Electric potential refers to the work needed to move a unit charge from a reference point to a specific point in an electric field.
Its units are joules per coulomb (J/C), more commonly known as volts (V).
Suppose we have a source charge Q and a test charge q.
We know that W = FΔd, and in this case, F = qE. This means W=qEΔd. Dividing both sides by q, we get W/q = EΔd.
However, W/q equals electric potential V. Thus, we have V = EΔd.
From this, we find that electric fields can also be expressed in terms of volts per meter (V/m).
Because ε = kQ/r2 and we set d = r, we have:
V = kQ/r2 * r
V = kQ/r
Voltage
Voltage refers to the change in electric potential between two points in an electric field. It is also known as electric potential difference. It is represented by ΔV, and its units are also volts (V).
To derive the formula for voltage, we start with ΔV = ΔEE/q. Here, ΔEE represents change in electric potential energy. Because electric fields do work by converting electric potential energy into kinetic energy, we have:
ΔEE = -W = -qEΔd
From this, we have:
ΔV = ΔEE/q
ΔV = -qEΔd/q
ΔV = -EΔd
Electric Potential Energy

To derive the formula for electric potential energy for a test charge q with respect to a source charge Q, we start with EE = qV. Then, we have:
EE = q(kQ/r)
EE = kQq/r
The Millikan Oil Drop Experiment
The Millikan oil drop experiment was an experiment conducted by Robert Millikan and Harvey Fletcher, in an attempt to determine the smallest unit of electric charge in nature.
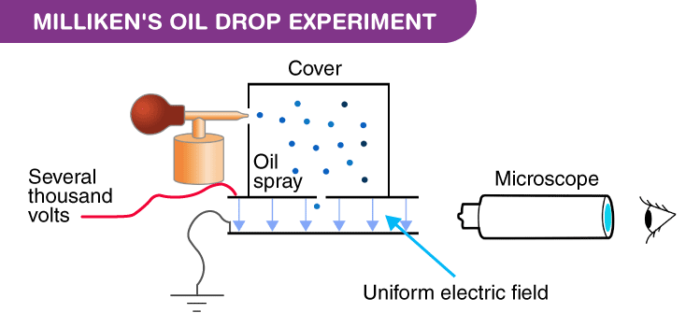
First, he sprayed a fine mist of oil particles between two parallel plates. Then, he used a microscope to observe their descent and measured the particles' terminal velocity, which he used to calculate their radii.

Then, he charged the oil particles using X-rays and applied an electric field onto the charged particles.
This field provided an upwards electric force, which eventually caused the particles to be suspended in midair.
Then, by equating the electric and gravitational forces using qE = mg, which becomes q(V/Δd) = mg, he was able to find the charged carried by each oil drop.
He found that each drop carried a charge that is an integer multiple of roughly 1.6 * 10-19 C.
Applications of Electric Fields
Electronics
Electric fields are central to the behavior of circuit components (e.g., capacitors, transistors).
Chemical Reactions

Electric fields govern the behavior of charged particles like protons and electrons, which forms the basis of all of chemical reactions.
Defibrillators

These devices restore or regulate heart functions by applying controlled electric fields to the heart.
Magnetic Fields
What Are Magnetic Fields?
A magnetic field is a region in space around a magnetic object or moving electric charge in which other such objects experience a force.
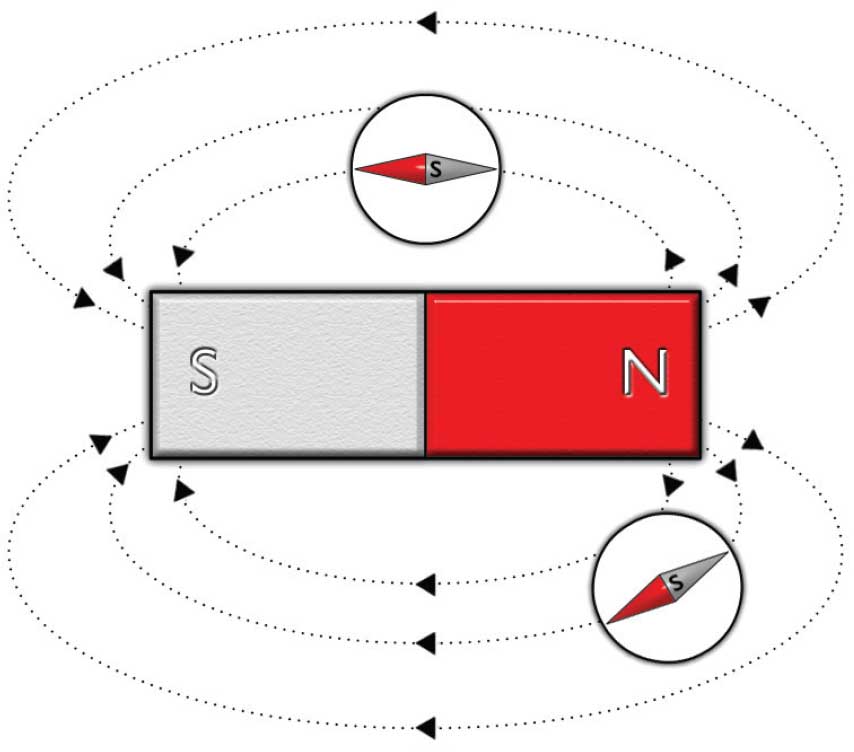
By convention, magnetic field lines outside a magnet point from the north pole (N) to the south pole (S) of the magnet. Inside the magnet, they point from S to N.
In general, the "direction" of the magnetic field at any given point is the direction in which a compass needle would point if it was placed at that point.
Conventional Current vs Electron Flow
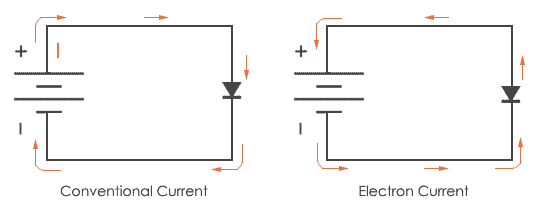
Conventional current is defined as current flowing from the positive terminal of the power source to its negative terminal. When electricity was discovered, it was initially thought to flow in such a manner.
Electron flow, on the other hand, describes the true behavior of electric current: flowing from negative to positive.
This distinction is important because the type of current involved will determine whether to use right-hand rules or left-hand rules in any given situation.
The right and left hand rules are conventions used to determine the direction of a magnetic field from the direction of a known type of current (or vice versa), and to determine the direction of a force on a moving charge exerted by a magnetic field.
Right and Left Hand Rules
Right Hand Rule For Straight Conductors

Point your right thumb in the direction of conventional current and curl your other fingers.
The direction in which your fingers point (base to tip) represents the direction of the magnetic field.
Right Hand Rule For Solenoids (Coils)

Point your right thumb in the direction of the magnetic field (your thumb is where the north pole is) and curl your other fingers.
The direction in which your fingers point represents the direction of conventional current.
Fleming's Right Hand Rule
Point your right thumb in the direction of the motion of the positively charged particle and point your other fingers in the direction of the magnetic field.
The direction in which your palm faces represents the direction of the magnetic force.
Left Hand Rules
These are functionally identical to the right hand rules and are used in the exact same way. However, they are used when dealing with electron flow or negatively charged particles.

Into/Out of Page Direction Symbols
Sometimes, we have to depict 3D situations on paper, which is 2D. As a result, we also use "into/out of page" symbols to show the directions of current, magnetic field, and force.
A circle with a dot in the middle (⊙) represents "out of the page", while a circle with a cross (⊗) represents "into the page".
When "dots" or "crosses" are drawn in a grid-like fashion on a page, it indicates that the magnetic field's direction is "out of the page" or "into the page", respectively.
Formulas for Magnetic Force
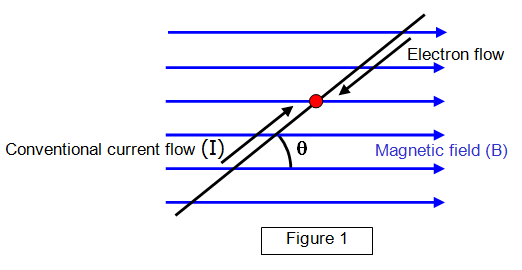
The formula for the force exerted on a moving charge by an external magnetic field is:
FM = Bqv(sinθ)
Here:
- B is the magnetic field in teslas
- q is the particle's charge in coulombs
- v is the particle's velocity
- θ is the angle between the velocity
and magnetic field vectors
The formula for the force exerted on a current-carrying wire by an external magnetic field is:
FM = ILB(sinθ)
Here:
- B is the magnetic field in teslas
- L is the wire's length in meters
- I is the current in amperes
- θ is the angle between the velocity
and magnetic field vectors
Applications of Magnetic Fields
Maglev Trains

Magnetic levitation (maglev) trains use extremely strong magnets (often superconducting magnets) to levitate and propel the train through the air, enabling speeds exceeding 400 km/h.
Particle Accelerators

Particle accelerator like the LHC use large, superconducting electromagnets to create powerful magnetic fields capable of keeping charged particles in a circular path.
MRI
Magnetic resonance imaging (MRI) uses a strong magnetic field to change the alignment the hydrogen atoms within the patient's body (most aligned towards, a few against). Then, a radiofrequency pulse excites these atoms, creating signals that a computer processes to generate an image.
Relationships Between Different Types of Fields
Gravitational and Electric Fields
Gravitational and electric forces share a number of parallels in terms of their properties, as shown in the chart below:

Electric and Magnetic Fields

Maxwell's equations state that a changing electric field produces a magnetic field, and that a changing magnetic field produces an electric field.

When an electric charge is accelerated, it produces a changing magnetic field. This changing magnetic field produces a changing electric field.
This cycle keeps on repeating, eventually forming a wave known as an electromagnetic wave.

Electromagnetic waves are categorized by their frequencies.
Gravitational and Magnetic Fields

Gravitational lensing occurs when massive objects bend light, which, as mentioned above, consists of both oscillating electric and magnetic fields.
Gravitational, Electric, and Magnetic Fields
There are some situations in which gravitational, electric, and magnetic fields play active roles simultaneously.
One such situation is the propagation of cosmic rays through space.
Cosmic rays are high-energy particles traveling through space at nearly the speed of light.
The gravitational fields of massive bodies (e.g., stars, black holes) can deflect these particles.
Environments like supernova remnants also produce strong electric fields, which help further accelerate cosmic ray particles.
The high speeds of cosmic ray particles come from strong magnetic fields in space (e.g., from supernova explosions or black holes).