FUNCIÓN Y RELACIÓN
la recolección de datos acerca de diferentes situaciones, se basa en la idea de relacionar elementos de dos conjuntos.
Todo elemento de X se relacione con un elemento de Y.
La relación de un elemento de X con un elemento de Y sea única
Los elementos de X se le asigna más de un elemento de Y ó no se le asignan

Tres elementos
Regla
Conjunto X ó A
El dominio de la función
Conjunto Y ó B
El Codominio de la función
El Rango
c
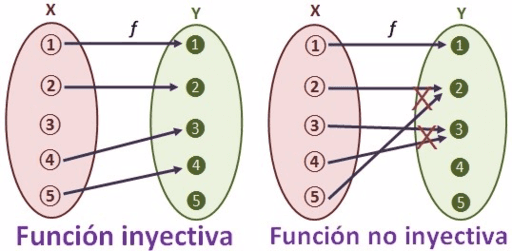
Función Inyectiva
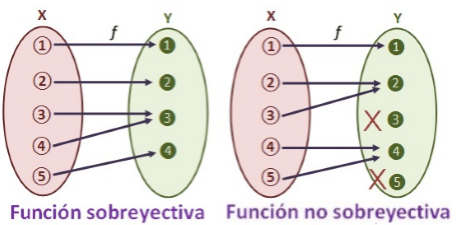
Función Suprayectiva
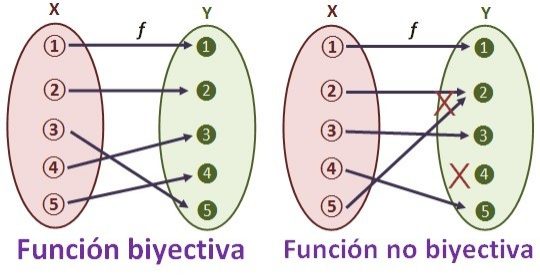
Función Biyectiva
Funciones algebraicas
Las funciones que se obtienen cuando se realizan sumas, restas y productos con las funciones constante e identidad
Función constante
Una función que toma K como constante y su dominio son todos los números reales
F(x) = K
Función identidad
una función donde la variable dependiente toma el mismo valor de la independiente
F(x)= X
son parte
Funciones polinómicas

Funciones Cuadráticas

Funciones lineales

Función Racional
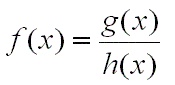
El cociente de dos funciones polinómicas
Funcion Irracional
aquellas cuyas expresiones matemáticas tienen radicales
A trozos
que poseen un dominio definido por varios intervalos
Funciones Trascendentes
aquellas funciones que no son algebraicas

Trigonométricas

trigonométricas inversas

exponenciales
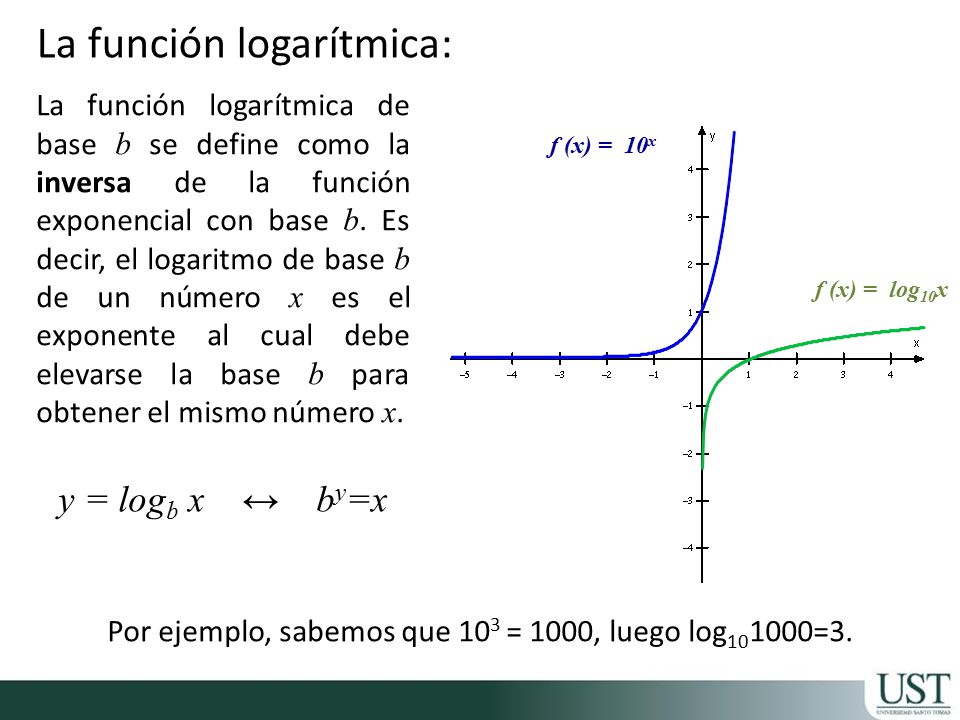
logarítmicas