funciones y relaciones

¿Qué es función?
Una función es un objeto matemático que se utiliza para expresar la relación entre dos magnitudes y se puede expresar de diversas formas ... Estas magnitudes, ya sean calculadas de antemano o medidas en un experimento, se pueden asignar de diversas formas .
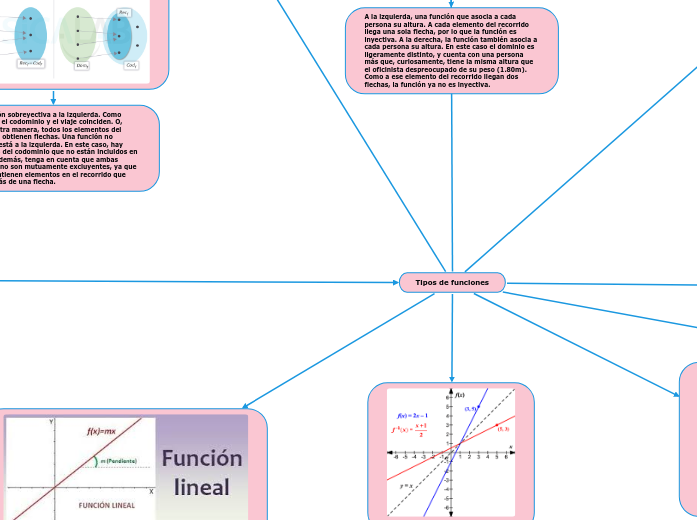
¿Qué es relacion?
Una relación es la correspondencia de elementos entre dos grupos. Una función es una relación en la que cada elemento de un conjunto (A) corresponde a uno y solo un elemento de otro conjunto (B). Cada función tiene su propio dominio y contradominio.
Tipos de relaciones
Simetrica
Se dice que R es simétrica si cada vez que un par (a, b) ∈ R, entonces el par (b, a) ∈ R
también (dicho de otra manera, ∀ a, b ∈ A, a R b ⇒ b R a). En términos del grafo de la
relacion, R es simétrica si por cada flecha que une dos vértices en un sentido, hay una
flecha (entre los mismos vértices) en el sentido opuesto.
Antisimetrica
Se dice que R es antisimetrica si cada vez que un par (a, b) ∈ R con a ̸= b, entonces el
par (b, a) ∈ R/ (dicho de otra manera, ∀ a, b ∈ A, a R b y b R a ⇒ a = b). En términos
del grafo de la relacion, R es antisimetrica si no hay ningún par de flechas en sentidos
opuestos que unen dos vértices distintos.
Transitiva
Se dice que R es transitiva si para toda terna de elementos a, b, c ∈ A tales que (a, b) ∈ R
y (b, c) ∈ R, se tiene que (a, c) ∈ R tambi´en (dicho de otra manera, ∀ a, b, c ∈ A, a R b y
b R c ⇒ a R c). En t´erminos del grafo de la relaci´on, R es transitiva si hay un “camino
directo” por cada “camino con paradas”.
Relaciones en un conjunto
Si dos o más conjuntos tienen los mismos elementos, determinamos que son iguales. Recuerde que el orden de los elementos en un conjunto no tiene nada que ver con su igualdad. No importa si los elementos se repiten.
Ejemplo
Las relaciones R6 y R7 arriba son relaciones en el conjunto R.
La igualdad de elementos siempre es una relacion en cualquier conjunto A: R = {(a, a), a ∈ A}, es decir ∀ a, b ∈ A : a R b ⇔ a = b.
Elementos de una funcion
Los dos elementos principales de una función son los posibles valores que tomarían ambas variables (dependientes e independientes).

Dominio
El dominio de la función es el conjunto de partida o el conjunto de los valores que pueden tomar la variable independiente (la llamamos x). La imagen, rango o recorrido de la función se incluye en el conjunto de llegada, que es una colección de valores que se pueden usar para tomar la variable dependiente (yof (x)).
¿Cómo se calcula?
Para determinar el dominio de una función, primero debemos determinar los valores de x para los cuales existe la función. Alternativamente, debemos determinar para qué valores de x no existe la función y permanecer con los valores de x donde la función sí existe. El tipo de función determina el dominio de esa función.
Codominio
El codominio es una colección de valores posibles. En realidad, el Codominio es parte de la definición de la función. El rango es el conjunto de valores que realmente existen. Por ejemplo, puede definir una función f (x) = 2x con el dominio y codominio del enteros (porque eligió como).
¿Cómo se calcula?
Ejemplo
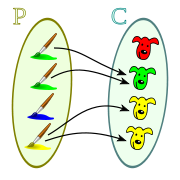
• El conjunto "A" es el Dominio,
• El conjunto "B" es el Codominio,
• Y el conjunto de elementos que se señalan en B (los valores reales producidos por la función) son el Rango, también llamado la Imagen.
Y tenemos:
Dominio: {1, 2, 3, 4}
Codominio: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Rango: {3, 5, 7, 9}


Rango
es el conjunto de números que dependen de la sustitución (tabulación) de los valores que pueden tomar "x", es decir, del dominio. Este grupo de números se conoce como "rango" y está ubicado en el eje "y" (abcisas).
¿Cómo se calcula?
Este es el rango de los datos. Para encontrar el rango, restamos el valor mínimo del conjunto de datos del valor máximo. Por ejemplo, en los datos de 2, 5, 3, 4, 5, y 5, el valor mínimo es 2 y el valor máximo es 5, entonces el rango es 5 – 2, o 3.
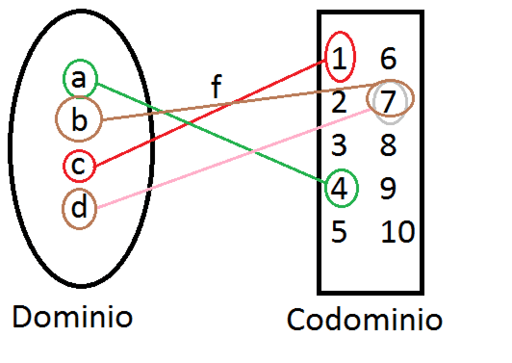
Grafica de una función
La gráfica de una función es la colección de puntos en el plano de la forma (x, y), donde x está bajo el control de la función e y = f (x).
Conocer la gráfica de una función permite conocer su imagen y su comportamiento lo cual puede ser muy útil al estudiar un fenómeno modelado por tal función. Una forma de obtener la gráfica de una función es tabular algunos puntos y luego unirlos. Obtengamos por ejemplo, las gráficas de las funciones que vimos en los ejemplos anteriores:
Tipos de funciones
Función inyectiva
Una función es inyectiva cuando no hay dos elementos del dominio que tengan la misma imagen. Formalmente:
∀a,b ∈ Domf , si f(a)= f(b)⇒a=b
Es decir, para cualquiera dos elementos a y b, pertenecientes al dominio de la función Domf, si sus imágenes f(a) y f(b) son iguales, los elementos son necesariamente iguales.
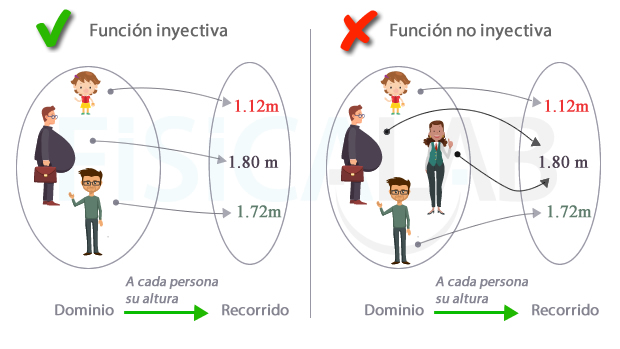
A la izquierda, una función que asocia a cada persona su altura. A cada elemento del recorrido llega una sola flecha, por lo que la función es inyectiva. A la derecha, la función también asocia a cada persona su altura. En este caso el dominio es ligeramente distinto, y cuenta con una persona más que, curiosamente, tiene la misma altura que el oficinista despreocupado de su peso (1.80m). Como a ese elemento del recorrido llegan dos flechas, la función ya no es inyectiva.
Función suprayectivas y biyectivas
Una función es sobreyectiva, también llamada suprayectiva o exhaustiva, cuando el codominio y el recorrido coinciden. Formalmente:
∀y ∈ Codf ∃x ∈ Domf / f(x)=y
Es decir, para cualquier elemento y del codominio existe otro elemento x del dominio tal que y es la imagen de x por f.
Las funciones reales son sobreyectivas cuando Recf=ℝ, ya que, por definición, en ellas Codf=ℝ.
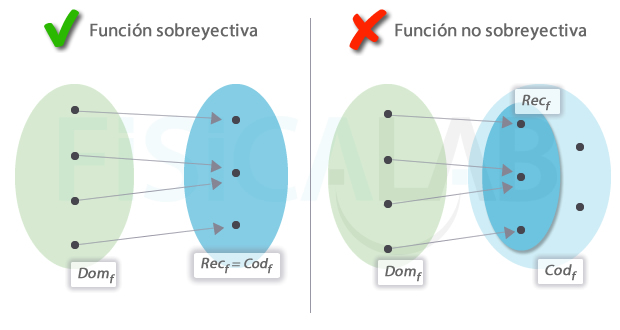
Una función sobreyectiva a la izquierda. Como resultado, el codominio y el viaje coinciden. O, dicho de otra manera, todos los elementos del codominio obtienen flechas. Una función no soberana está a la izquierda. En este caso, hay elementos del codominio que no están incluidos en el viaje. Además, tenga en cuenta que ambas funciones no son mutuamente excluyentes, ya que ambas contienen elementos en el recorrido que reciben más de una flecha.
Funciones especiales
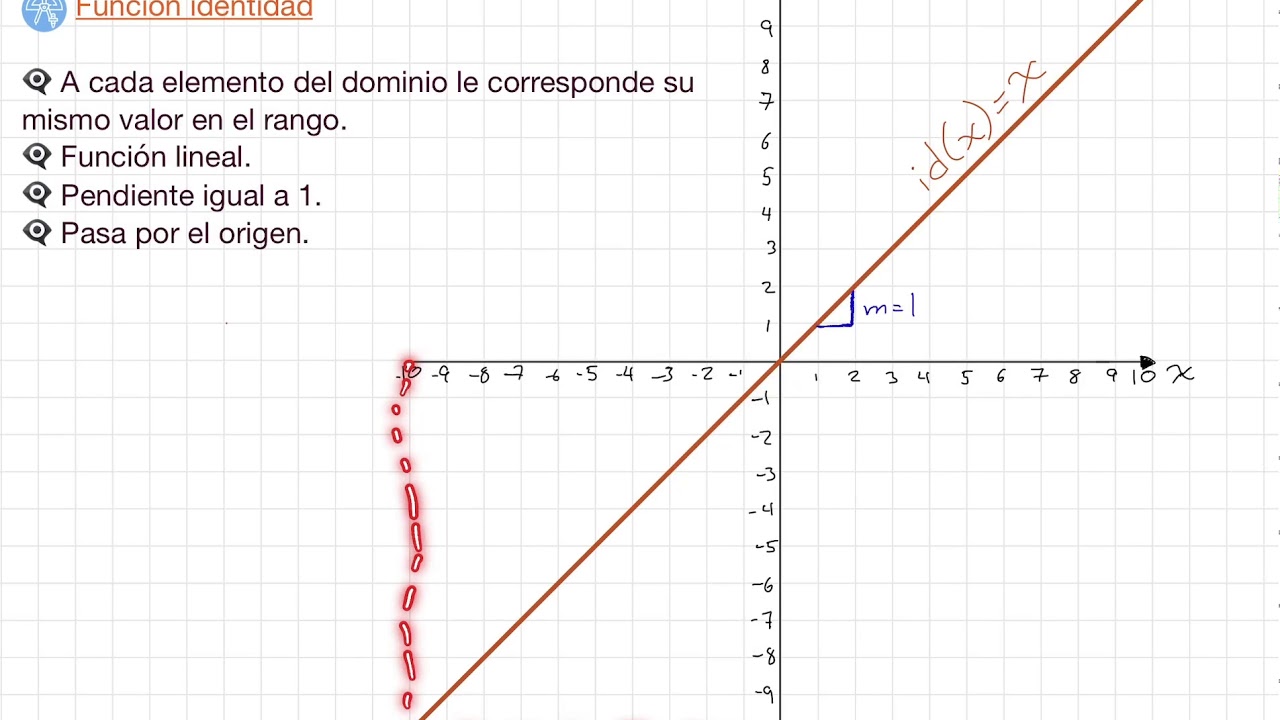
Idéntica o identidad
Es aquella cuya gráfica es una recta que pasa por el origen, de los ejes coordenadas y su pendiente es m=1
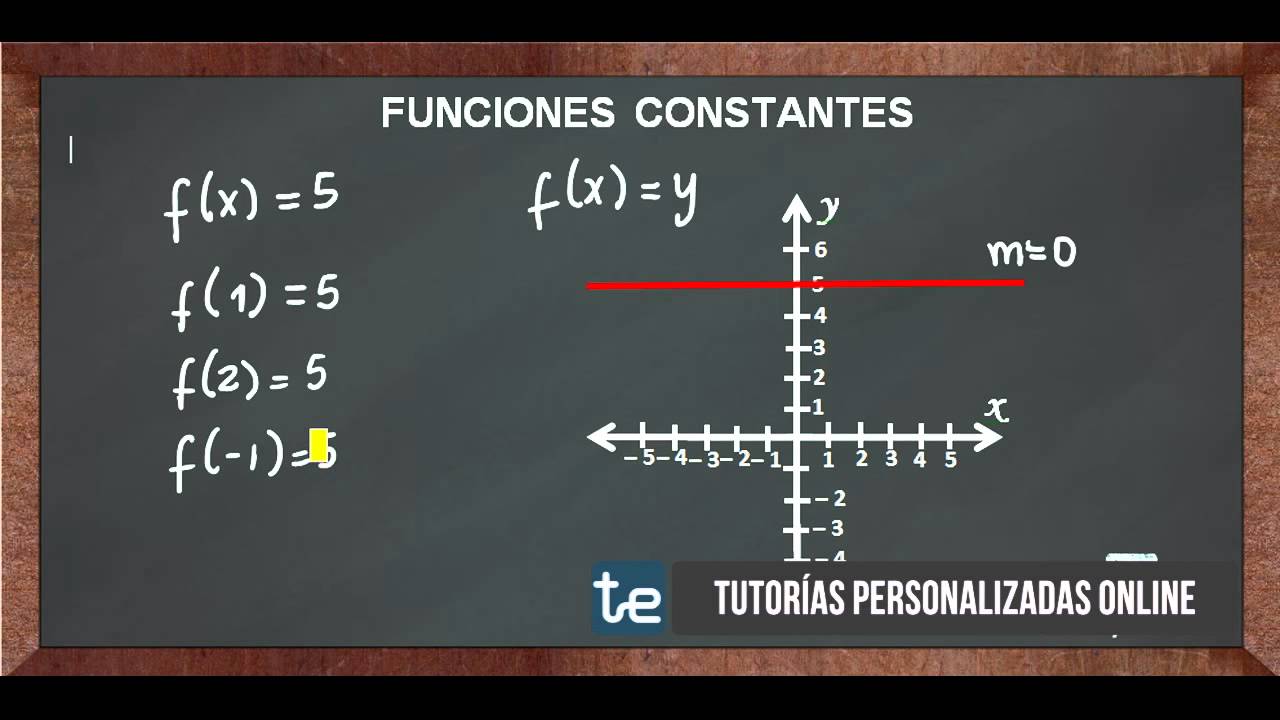
Constante
Es aquella cuyo valor no depende de ninguna variable, y se puede representar como
una función matemática de la forma: f(x)=h donde h hace parte de los números reales
y además es una constante.
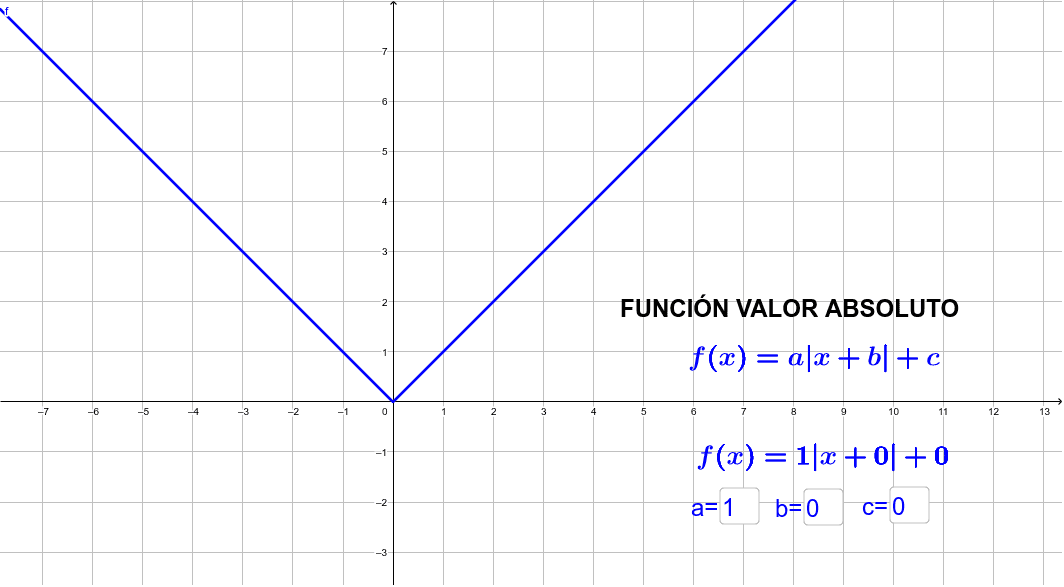
Valor absoluto
Una función de valor absoluto es una función que contiene una expresión algebraica dentro de los símbolos de valor absoluto. Recuerde que el valor absoluto de un número es su distancia desde 0 en la recta numérica

Por parte o trozos
es una función cuya definición, llamada regla de correspondencia, cambia dependiendo del valor de la variable independiente.Formalmente, una función real f de una variable real x es la relación cuya definición está dada por varios conjuntos disjuntos de su dominio.
Función lineal
Una función lineal es aquella cuya expresión algebraica es del tipo y = mx,siendo m un número cualquiera distinto de 0. Su gráfica es una línea recta que pasa por el origen, (0,0).

Funcion inversa
La función inversa (o recíproca) de f (denotada por f-1) es la que invierte el camino, asignando elementos de Y a elementos de X. También podemos definir una función inversa basada en la composición de la función. Para que se invierta una función f, debe ser inyectiva.

Función exponencial
El término "exponencial" se refiere a un número positivo que se incrementa con una variable x, como: A pesar de que la función exponencial en matemáticas es (e = 2.718281), esta función se abrevia comúnmente como exp (x), y se conoce como "lo exponencial de x".

Función logarítmica
Se llaman funciones logarítmicas a las funciones de la forma f(x) = loga(x) donde "a" es constante (un número) y se denomina la base del logaritmo. Seguramente ya se han estudiado los logaritmos por lo que conoces la deficición de logaritmo de un número (b) en una cierta base (a): loga(b)=n si se cumple que an=b.

Función trigonométrica
Las funciones trigonométricas son las funciones de un ángulo. Estas usualmente incluyen términos que describen la medición de ángulos y triángulos, tal como seno, coseno, tangente, cotangente, secante y cosecante.
Los ángulos en las funciones trigonométricas se expresan como radianes. Los radianes son el equivalente de los grados de los ángulos en función del radio de la circunferencia.
Un rectángulo triángulo es un polígono de tres lados con un ángulo recto (equivalente a 90*). Los lados que definen el arco se conocen como catetos, y el lado opuesto de mayor longitud se conoce como hipotenusa.
función de seno, coseno, tangente, cotangente, cosecante, secante
el seno (se abrevia sen) es la razón o la división de la longitud del cateto opuesto (CO) entre la longitud de la hipotenusa (H)
el coseno (se abrevia cos) es la razón entre la longitud del cateto adyacente (CA) entre la longitud de la hipotenusa (H)
la tangente (se abrevia tan) es la razón entre la longitud del CO entre el CA, esto es igual a la división del seno entre el coseno
la cotangente (se abrevia cot) es la razón entre el CA y el CO
la secante (se abrevia sec) es la razón entre la hipotenusa y el CA, y
la cosecante (se abrevia csc) es la razón entre la hipotenusa y el CO.