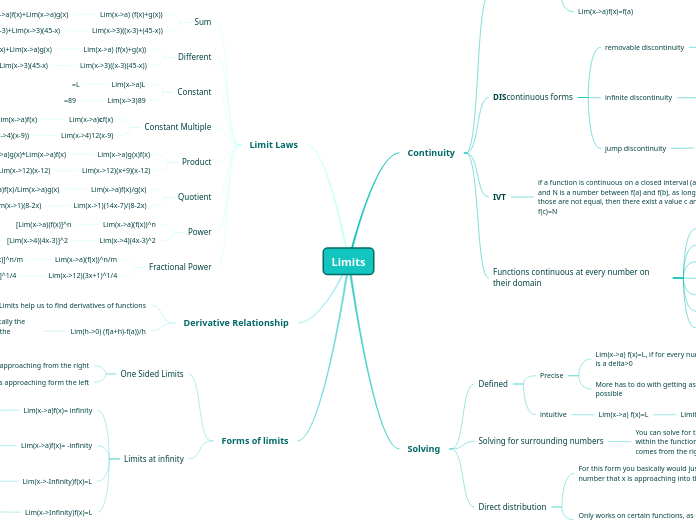
Limits
Continuity
Requirements
f(a) is defined
Lim(x->a)f(x) exists
Lim(x->a)f(x)=f(a)
DIScontinuous forms
removable discontinuity
we can redefine F(x) at a just as a single value
lim(x->a)f(x)=L
f(a)=DNE
Lim(x->a)f(x)does not = f(a)
infinite discontinuity
funtion goes to infinity or -infinity at a
f(a)= may be defined
Lim(x->a)f(x)does not = f(a)
lim(x->a)f(x)=infinity (not a real number)
jump discontinuity
limits form the left and right exist but are not the same
f(a)= may be defined
Lim(x->a)f(x)does not = f(a)
lim(x->a)f(x)=DNE
IVT
if a function is continuous on a closed interval (a,b) and N is a number between f(a) and f(b), as long as those are not equal, then there exist a value c and f(c)=N
Functions continuous at every number on their domain
Polynomials
Trig functions
Exponential functions
rational functions
inverse trig functions
log functions
root funtions
Solving
Defined
Precise
Lim(x->a) f(x)=L, if for every number epsilon>0 there is a delta>0
if 0<|x-a|<delta the n |f(x)-L|,epsilon
More has to do with getting as close to the value as possible
Delta, along x-axis
How much room around that x value
Epsilon, along y-axis
room around the y value
intuitive
Lim(x->a) f(x)=L
Limit of f(x) as x approaches a is L
Solving for surrounding numbers
You can solve for the numbers surrounding that limit within the function, but this only holds true if it comes from the right and left
if Lim(x->3)f(x)
solve for x=2.9999, x=3.001
Direct distribution
For this form you basically would just substitute the number that x is approaching into the function
Only works on certain functions, as long as a is in the domain of f
Polynomial
Lim(x->a)x^2-3x+1=a^2-3a+1
Lim(x->4)x^2-3x+1=4^2-3(4)+1
16-12+1=5
Rational
Lim(x->a)1/x-3=1/a-3
Lim(x->8)1/x-3=1/8-3
=1/5
Trig Functions
Lim(x->a)cosx=cosa
Lim(x->0)cosx=cos(0)
=1
Transcendental
Lim(x->a)2^x=2^a
Lim(x->3)2^x=2^3
=8
Limit Laws
Sum
Lim(x->a) (f(x)+g(x))
Lim(x->a)f(x)+Lim(x->a)g(x)
Lim(x->3)((x-3)+(45-x))
Lim(x->3)(x-3)+Lim(x->3)(45-x)
0+42=42
Different
Lim(x->a) (f(x)+g(x))
Lim(x->a)f(x)+Lim(x->a)g(x)
Lim(x->3)((x-3)(45-x))
Lim(x->3)(x-3)-Lim(x->3)(45-x)
0+42=42
Constant
Lim(x->a)L
=L
Lim(x->3)89
=89
Constant Multiple
Lim(x->a)cf(x)
c(Lim(x->a)f(x)
Lim(x->4)12(x-9)
12(Lim(x->4)(x-9))
12(-5)=-60
Product
Lim(x->a)g(x)f(x)
Lim(x->a)g(x)*Lim(x->a)f(x)
Lim(x->12)(x+9)(x-12)
Lim(x->12)(x+9)*Lim(x->12)(x-12)
21*0=0
Quotient
Lim(x->a)f(x)/g(x)
Lim(x->a)f(x)/Lim(x->a)g(x)
Lim(x->1)(14x-7)/(8-2x)
Lim(x->1)(14x-7)/Lim(x->1)(8-2x)
=7/6
Power
Lim(x->a)(f(x))^n
[Lim(x->a)(f(x)]^n
Lim(x->4)(4x-3)^2
[Lim(x->4)(4x-3)]^2
(13)^2=169
Fractional Power
Lim(x->a)(f(x))^n/m
[Lim(x->a)(f(x)]^n/m
Lim(x->12)(3x+1)^1/4
[Lim(x->12)(3x+1)]^1/4
(37)^1/4=2.466
Derivative Relationship
Limits help us to find derivatives of functions
Lim(h->0) (f(a+h)-f(a))/h
finding the limit as h approaches 0 is typically the last step within the process when finding the derivative of a function at a certain point
Forms of limits
One Sided Limits
Limits approaching from the right
Lim(x->a+)f(x)
Limit of f(x) as x approaches a from the right
Limits approaching form the left
Lim(x->a-)f(x)
Limit of f(x) as x approaches a from the left
Limits at infinity
Lim(x->a)f(x)= infinity
creates a vertical asymptote at x=a as the values surrounding a, become significantly larger as it approaches a
Lim(x->a)f(x)= -infinity
creates a vertical asymptote at x=a as the values surrounding a, become significantly negative as it approaches a
Lim(x->-Infinity)f(x)=L
f(x) comes really close to L as it becomes significantly more negative, creating a horizontal asymptote at y=L
Lim(x->Infinity)f(x)=L
f(x) comes really close to L as it becomes significantly larger, creating a horizontal asymptote at y=L