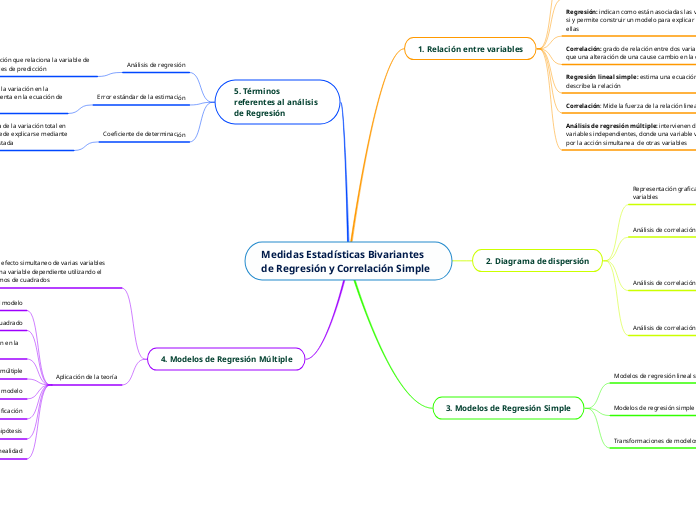
Medidas Estadísticas Bivariantes de Regresión y Correlación Simple
1. Relación entre variables
Relación funcional: relación matemática exacta entre dos variables
Relación estadística: existe una relación aproximada entre las dos variables
Regresión: indican como están asociadas las variables entre si y permite construir un modelo para explicar la relación entre ellas
Correlación: grado de relación entre dos variables sin suponer que una alteración de una cause cambio en la otra variable
Regresión lineal simple: estima una ecuación lineal que describe la relación
Correlación: Mide la fuerza de la relación lineal
Análisis de regresión múltiple: intervienen dos o mas variables independientes, donde una variable viene explicada por la acción simultanea de otras variables
2. Diagrama de dispersión
Representación grafica de la existencia de relación entre las variables
Análisis de correlación
Mide el grado de relación entre las variables
Mide la cercanía de la relación entre dos o mas variables
Análisis de correlación simple
Mide la relación entre solo una variable independiente (X) y la variable dependiente (Y)
Determina la cantidad de variación conjunta que presenta dos variables aleatorias de una distribución bidimensional
Análisis de correlación múltiple
Muestra el grado de asociación entre dos o mas variables independientes y la variable dependiente
3. Modelos de Regresión Simple
Modelos de regresión lineal simple
Modelos de regresión simple no lineales
Modelo cuadrático
Modelo cubico
Transformaciones de modelos de regresión no lineales
Modelos exponenciales
5. Términos referentes al análisis de Regresión
Análisis de regresión
Se usa para derivar una ecuación que relaciona la variable de criterio con una o mas variables de predicción
Error estándar de la estimación
Se refiere al valor absoluto de la variación en la variable de criterios que no cuenta en la ecuación de regresión ajustada
Coeficiente de determinación
Denota la proporción relativa de la variación total en la variable de criterio que puede explicarse mediante la ecuación de regresión ajustada
4. Modelos de Regresión Múltiple
Permite averiguar el efecto simultaneo de varias variables independientes en una variable dependiente utilizando el principio de los mínimos de cuadrados
Aplicación de la teoría
Desarrollo del modelo
Se emplea el método de mínimo cuadrado
Los coeficientes estimados se identifican en la salida de los programas informáticos
El coeficiente de determinación es múltiple
Supuestos del modelo
Pruebas de significación
Regla de decisión del contraste de hipótesis
El problema de la multicolinealidad