POTENCIAS, RAICES, LOGARÍTMOS Y NOTACIÓN CIENTIFICA
OPERACIONES INVERSAS

RAICES
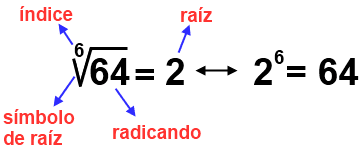
La radicación:
Operaci{ion inversa a la potenciación nos permite averiguar cuál fue la base que se elevó al indice del radical "n" para que dé como resultado el radicando.
En el ejemplo de la imágen, se pretende averiguar cuál fue la base que al elevarse a la 6 dá como resultado 64, en ese caso la respuesta es 2, porque: 26 = 64
Propiedades

Racionalización

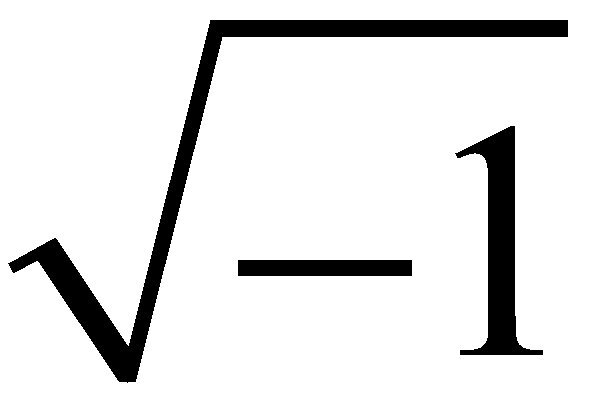
Raíces de indice par
y radicando negativo

Números Imaginarios y complejos
Definición

La ecuación x2+a=0 con “a” un número real positivo, no tiene solución en el conjunto de los números reales porque el cuadrado de un número real siempre es positivo y al ser sumado con un número positivo su resultado no puede ser igual a cero, explicado de otra manera, las raíces con índice par de números negativos, no tienen solución en el conjunto de los reales (R). Para dar solución a este tipo de ecuaciones, se generó un nuevo conjunto numérico denominado, números imaginarios.
La unidad principal o unidad imaginaria está representada por la letra “i” y está definida como aparece en la imágen.
Potencias de i

i0 = 1; todo número elevado a la cero = 1
i1 = i; todo # elevado a 1 es el mismo #.
i2 = -1; De la definición de imaginario.
i3 = -i; producto de i.i2 = i.(-1) = -i.
i4 = 1; producto de i2.i2 = (-1).(-1) = 1
De manera que cada potencia de 4 el ciclo se repite.
i9 = i; producto i4.i4.i = 1.1.i = i
Representación
Binomial

Un número complejo esta formado por una parte real y una parte imaginaria: Z = x + yi
Ej. Sea "Z" el número complejo Z = 4 + 3i, donde 4 es la parte real (R) y 3 la parte imaginaria (i)
Cartesiana
La forma cartesiana es representar el número complejo como un par ordenado donde la primera componente es la Real y la segunda es la Imaginaria, (R, i).
Para el ejemplo el complejo Z = 4+3i se ve dibujado en la imagen por el par ordenado (4, 3)
Polar

La forma polar de expresar un complejo es mediante la norma o distancia del vector que se forma en el plano cartesiano y el ángulo que forma con la horizontal positiva.
La norma se obtiene por pitagoras ya que es la hipotenusa del triángulo rectángulo que se forma: |Z|=Raiz(R2 + i2).
El ángulo se obtiene trigonometricamente como: ángulo = ArcTang (i/R) = Tang-1 (i/R)

Operaciones
Suma/Resta
La suma o resta de complejos es otro número complejo, solo se realiza las operaciones por separado, por un lado los Reales y da el resultado Real y por otro lado con los imaginarios.
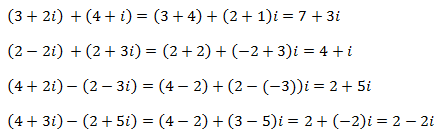
Multiplicación
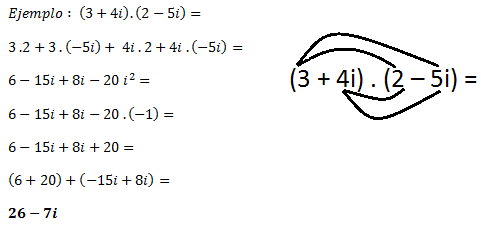
El producto de dos números complejos se realiza como dos binomios normales, en el resultado se suman los Reales y los imaginarios y el término i2; se opera con su valor equivalente (-1) y se opera con los Relaes
División

Conjugado y opuesto
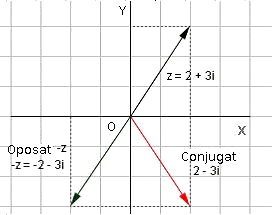
Se puede observar que para el complejo:
Z = 2+3i, su conjugado, es equivalente a cambiar el signo solo del imaginario y se ve como un reflejo sobre el eje horizontal
Z conjugado = 2-3i, mientras que el opuesto a Z se cambian ambos signos y se ve en la imagen como el vector opuesto por el origen -Z = -2-3i

LOGARÍTMOS

Definición



Para tener en cuenta: Los logarítmos en base 10, solo se escribe la palabra Log y se sobre entiende que su base es 10.
Igualmente para Logarítmos Neperianos o Naturales, se expresan como Ln y tienen base "e" Número de Euler e = 2,71828...
POTENCIAS
Operación que permite expresar,en forma simplificada un producto de factores iguales.
Propiedades:
Reglas generales permiten simplificar expresiones algebraicas:
Exponentes Enteros +
Básicas
1n = 1
a0 = 1
a1 = a
Bases Iguales
Producto
Suman los exponentes y se deja la misma base.

División:
Se deja la misma base y se restan los exponentes.
an / am = an-m

Potencia de Potencias
Se deja la base y se multiplican los exponentes.
(an)m = an.m

Exponentes iguales
Se deja el exponente y se hace la operación indicada a realizar.
an.b.n = (a.b)n ó an/b.n = (a/b)n
Ej: 54.34 = (5.3)4 = 154
ó 83/43 = (8/4)3 = 23


Exponentes Enteros -
Toda potencia con exponente negativo es igual al inverso multiplicativo de la base, elevada al exponente positivo, es decir:
a-n = 1/an; 1/a-m = am; (a/b)-n = (b/a)n
Exponente Racional

Los exponentes racionales, surgen cuando una expresión radical se expresa como potencia, es decir:
En la expresión de la imagen tenemos "n" como indice radical y "m" como exponente de "a", y podemos observar que al representarse como una potencia, "a" se mantiene como base de la potencia, el exponente "m" representa el numerador y el indice radical "n" representa el denominador del exponente racional o fraccionario.
Para tener en cuenta:
Al trabajar con expresiones algebraicas, es importante descomponer los coeficientes en sus factores primos para una mejor interpretación de las propiedades de las potencias.
Ej: (48x+9)2.(18x2-8)3
(24.3.x+32)2.(2.32x2-23)3
(28.32.x2+34).(23.36x6-29)
211.38.x8 - 217.32x2 + 23.310.x6 - 29.34

Definición

La notación científica permite expresar esas cantidades como potencias en base 10 y exponentes enteros.Como por ejemplo las distancias interestelares, la memoria de un computador en bits, son cantidades muy grandes, mientras que el peso de los átomos, el diámetro de un glóbulo rojo, son cantidades muy pequeñas.
Un número está expresado en notación científica, si está escrito de la forma:
como lo muestra la imagen.

Así se expresa un número en notación científica. Múltiplos y submúltiplos de unidades de medida.
Operaciones






Ejemplos