PRODUCTOS NOTABLES
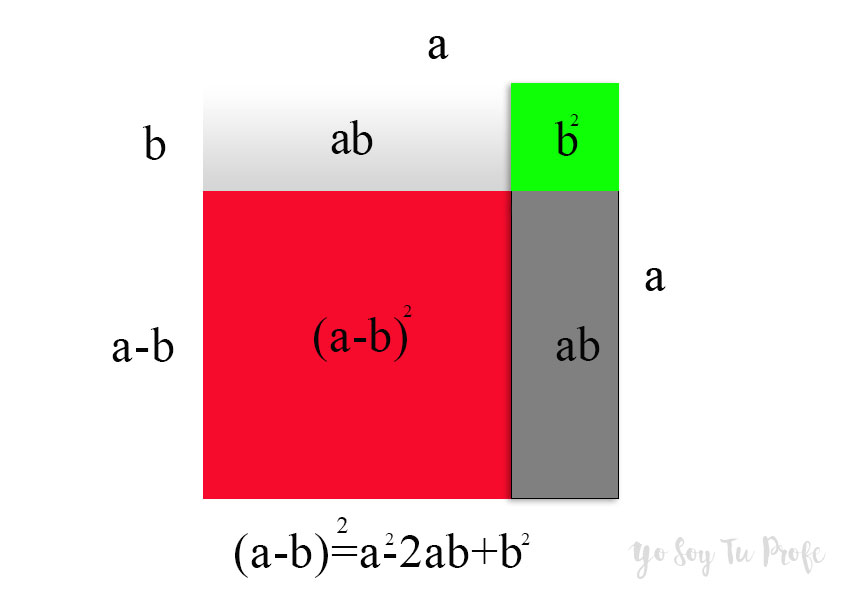
Cuadrado de una diferencia
CONCEPTO
es una de las identidades notables (o productos notables), es decir, consiste en una regla matemática que facilita el cálculo de elevar al cuadrado un binomio con dos términos: uno positivo y otro negativo.
Ejemplos
1) (x - 3)2= (x - 3)2 = x2 - 2·3·x + 32 = x2 - 6x + 9
2) (2x - 3y2)2= (2x - 3y2)2 = (2x)2 - 2·(2x)·(3y2) + (3y2)2 = 4x2 - 12xy2 + 9y4
3) 69^2= 692 = (70 - 1)2 = 702 - 2·70·1 + 12 = 4900 - 140 + 1 = 4761
Formula
(a-b)^2= a^2-2ab+b^2
Representación gráfica

Producto de la forma (x+a) (x+b)
CONCEPTO
Una expresión de la forma (x+a) (x+b) es igual al término común (x) al cuadrado más el producto del término común con la suma de los términos no comunes (a y b), más el producto de ,los términos no comunes.
Estas expresiones siempre se caracterizan por solo ser binomios.
Ejemplos
1) x² -7x -70+10x = x² + 3x -70
2) x² - 3x + 6 - 2x = x² - 5x + 6
3) x² + x + 4+4x = x² + 5x + 4
Representación gráfica

Formula
x² + (a+b)x + ab
Suma por diferencia
CONCEPTO
"suma por diferencia es igual a diferencia de cuadrados".
Es decir, que el resultado de multiplicar la suma de dos números por su diferencia es el mismo que si restamos los cuadrados de ambos números.
Formula
(a + b) (a - b) = a a - a b + b a - b b = a2 - b2
Ejemplos
1) (3x+2)(3x-2)
(3x+2)(3x-2)=(3x)2-22=9x2-4
2) (y3+5)(y3-5)
(y3+5)(y3-5)=(y3)2-52=y6-25
3) (4m5+8y)(4m5-8y)
(4m5 + 8y)(4m5-8y)=(4m5)2-(8y)2=16m10-64y2
Representación gráfica
Fuentes:
www.superprof.es
https://wikimat.es/polinomios/productos-notables/binomio-al-cubo/
http://es.onlinemschool.com/math/library/multiplication_formulas/sum2/
https://www.celeberrima.com/cuadrado-de-una-suma-con-ejemplos-resueltos/
https://www.superprof.es/diccionario/matematicas/algebra/binomio-cubo.html#:~:text=Qu%C3%A9%20significa%20binomio%20al%20cubo%20en%20Matem%C3%A1ticas&text=Un%20binomio%20al%20cubo%20(suma,m%C3%A1s%20el%20cubo%20del%20segundo.
Cuadrado de una suma
CONCEPTO
"el cuadrado de una suma es la suma de los cuadrados MÁS el doble del producto".
Es decir, que el resultado de elevar al cuadrado la suma de dos números es el mismo que si sumamos los cuadrados de ambos números y añadimos el doble de su producto.
Representación gráfica

Ejemplos
1) (x + 3)2
(x + 3)2 = x2 + 2·3·x + 32 = x2 + 6x + 9
2) (2x + 3y2)2
(2x + 3y2)2 = (2x)2 + 2·(2x)·(3y2) + (3y2)2 = 4x2 + 12xy2 + 9y4
3) Calcular 71^2
71^2 = (70 + 1)2 = 702 + 2·70·1 + 12 = 4900 + 140 + 1 = 5041
Formula
(a+b)^2= a^2+2ab+b^2
Cubo de un binomio
CONCEPTO
El cubo de un binomio o binomio al cubo, es una expresión algebraica, formada por dos términos que se pueden sumar o restar; y en la cual las operaciones de (suma o resta) estarán elevadas al cubo.
Formula
(x-a)^3= x^3-3x^2+3xa^2-a^3
Ejemplos
1) (x + 2)3 = x3 + 3 · x2 · 2 + 3 · x · 22 + 23
= x3 + 6x2 + 12x + 8
2) (3x − 2)3 = (3x)3 − 3 · (3x)2 · 2 + 3 · 3x · 22 − 23 =
27x 3 − 54x2 + 36x − 8
3) (2x + 5)3 = (2x)3 + 3 · (2x)2 ·5 + 3 · 2x · 52 + 53 =
8x3 + 60 x2 + 150 x + 125
Representación gráfica

Historia
Nacieron en Grecia, de aquí llegaron a Arabia, después a España y de esto a América.

Long-term goal
Características
Ayudan a hacer más fáciles los ejercicios algrebraicos.
Internamente poseen suma y resta de dos términos.
Formulas sencillas de recordar y realizar.
La formulas estan compuestas pricipalmente por la multiplicación y elevación a la potencia.
Usualmente lo que se usa en sus formulas son binomios.

Long-term goal
Definición
Son productos que cumplen reglas fijas y cuyo resultado puede ser escrito sin verificar la multiplicación

Long-term goal
Utilidad
Estos se usan cuando se busca aplica una reducción a un proceso matemático.
Para sacar principalmente la medida de una superficie y en la ingeniería para hallar el área.

Long-term goal
