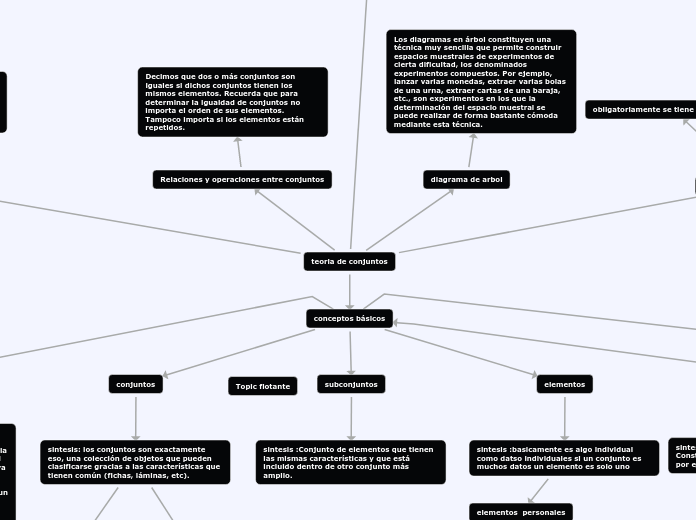
teoria de conjuntos
conceptos básicos
conjuntos
sintesis: los conjuntos son exactamente eso, una colección de objetos que pueden clasificarse gracias a las características que tienen común (fichas, láminas, etc).
conjunto de datos
los datos se toman como numeros en lalguna tabla o lugar donde se pongan los datos
conjuntos normales
cumple con las caracteristicas normales de un conjunto normal
subconjuntos
sintesis :Conjunto de elementos que tienen las mismas características y que está incluido dentro de otro conjunto más amplio.
elementos
sintesis :basicamente es algo individual como datso individuales si un conjunto es muchos datos un elemento es solo uno
elementos personales
los elementos personales pueden ser un dato no numerico
diagramas de Venn-Euler
Los diagramas de Venn proporcionan una forma clara y eficaz de mostrar visualmente las relaciones entre conjuntos de datos. Sirven como una ayuda visual útil en sesiones de lluvia de ideas, reuniones y presentaciones.
utilidades
basicamente organiza todo de manera clara y muy importante con referencias visuales
Relaciones y operaciones entre conjuntos
Decimos que dos o más conjuntos son iguales si dichos conjuntos tienen los mismos elementos. Recuerda que para determinar la igualdad de conjuntos no importa el orden de sus elementos. Tampoco importa si los elementos están repetidos.
diagrama de arbol
Los diagramas en árbol constituyen una técnica muy sencilla que permite construir espacios muestrales de experimentos de cierta dificultad, los denominados experimentos compuestos. Por ejemplo, lanzar varias monedas, extraer varias bolas de una urna, extraer cartas de una baraja, etc., son experimentos en los que la determinación del espacio muestral se puede realizar de forma bastante cómoda mediante esta técnica.
eventos complementarios
obligatoriamente se tiene que dar el otro
Eventos complementarios: son aquellos que si no se da uno,
teoria de la probabbilidad axiomas
Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función definida sobre un conjunto de sucesos determine consistentemente sus probabilidades. Fueron formulados por Kolmogórov en 1933.
axioma 1
La probabilidad de un evento no puede ser negativa
axioma 2
La probabilidad del evento seguro, es igual a 1, denotado simbólicamente
axioma 3
Si son eventos mutuamente excluyentes (es decir, su intersección es el conjunto vacío), entonces:
lo que debes saber
espacio muestral y eventos
sintesis:Espacio muestral discreto finito. Consta de un número finito de elementos, por ejemplo lanzar un dado.
tipos
espacio muestral discreto
Espacio muestral discreto infinito. Consta de un número infinito numerable de elementos, por ejemplo lanzar un dado hasta que salga un cinco.
espacio mustral continuo
Espacio muestral continuo. Consta de un número infinito no numerable de elementos, por ejemplo todas las medidas posibles de espárragos extraidos aleatoriamente de una población