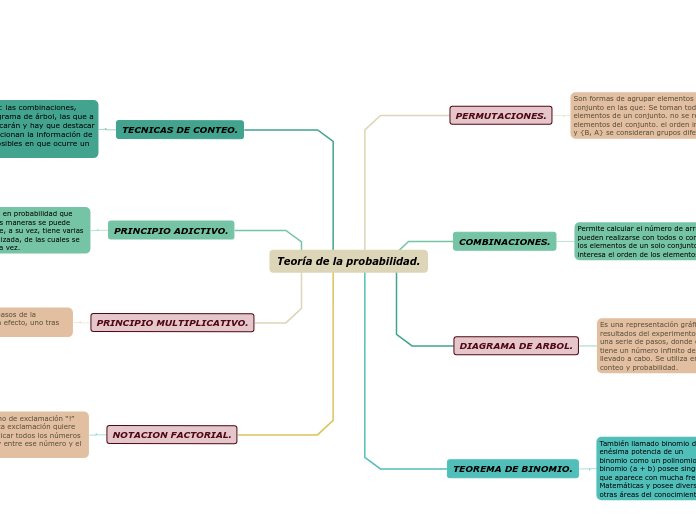
Teoría de la probabilidad.
PERMUTACIONES.
Son formas de agrupar elementos de un conjunto en las que: Se toman todos los elementos de un conjunto. no se repiten los elementos del conjunto. el orden importa ({A, B} y {B, A} se consideran grupos diferentes)
EJEMPLO.
Si tienes n cosas para elegir y eliges r de ellas, las permutaciones posibles son:
n × n × ... (r veces) = nr
DESPUÉS hay n posibilidades para la segunda elección.
Por ejemplo en la cerradura de arriba, hay 10 números para elegir (0,1,...,9) y eliges 3 de ellos:
10 × 10 × ... (3 veces) = 103 = 1000 permutaciones
COMBINACIONES.
Permite calcular el número de arreglos que pueden realizarse con todos o con una parte de los elementos de un solo conjunto, en donde no interesa el orden de los elementos entre sí.
EJEMPLO.
En las combinaciones, a diferencia de lo que sucedía con las permutaciones, el orden de los elementos no es importante.
La fórmula a aplicar es la siguiente: n Cr=n/(n-r)r
DIAGRAMA DE ARBOL.
Es una representación gráfica de los posibles resultados del experimento, el cual consta de una serie de pasos, donde cada uno de estos tiene un número infinito de maneras de ser llevado a cabo. Se utiliza en los problemas de conteo y probabilidad.
EJEMPLO.
Marcos y Enrique van a jugar un campeonato de tenis. El primero en ganar dos juegos seguidos o que gane un total de tres juegos, gana el torneo. El diagrama siguiente da varias formas en las cuales puede finalizar el campeonato.
RESOLUCIÓN :
Observemos que existen 10 puntos extremos, los cuales corresponden a las 10 maneras en que puede finalizar el campeonato : MM, MEMM, MEMEM, MEMEE, MEE, EMM, EMEMM, EMEME, EMEE, EE
TEOREMA DE BINOMIO.
También llamado binomio de Newton, expresa la enésima potencia de un
binomio como un polinomio. El desarrollo del binomio (a + b) posee singular importancia ya que aparece con mucha frecuencia en Matemáticas y posee diversas aplicaciones en otras áreas del conocimiento.
TECNICAS DE CONTEO.
Técnicas de conteo a: las combinaciones, permutaciones y diagrama de árbol, las que a continuación se explicarán y hay que destacar que éstas nos proporcionan la información de todas las maneras posibles en que ocurre un evento determinado.
PRINCIPIO ADICTIVO.
Es una técnica de conteo en probabilidad que permite medir de cuántas maneras se puede realizar una actividad que, a su vez, tiene varias alternativas para ser realizada, de las cuales se puede elegir solo una a la vez.
EJEMPLO
El principio aditivo nos dice que la cantidad de opciones o maneras de hacer esta elección es 8+25=33.
Este principio también se puede aplicar en el caso de que sea un único evento el involucrado, que a su vez tenga diferentes alternativas para ser realizado.
PRINCIPIO MULTIPLICATIVO.
Implica que cada uno de los pasos de la actividad deben ser llevados a efecto, uno tras otro.
NOTACION FACTORIAL.
se representa con un signo de exclamación “!” detrás de un número. Esta exclamación quiere decir que hay que multiplicar todos los números enteros positivos que hay entre ese número y el 1.
Es el producto de n entero positivo hasta 1. En algunos problemas de matemáticas se nos presentan multiplicaciones de números naturales sucesivos tal como: 4 x 3 x 2 x 1 = 24; 3 x 2 x 1 = 6; 2 x 1 = 2.