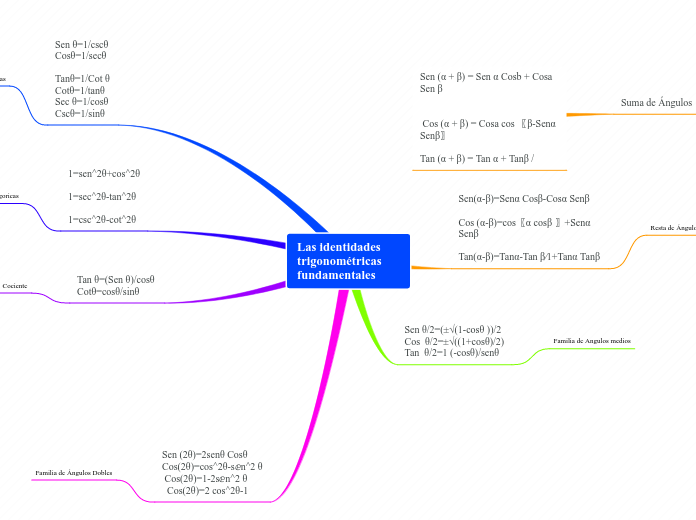
Las identidades trigonométricas fundamentales
Sen(α-β)=Senα Cosβ-Cosα Senβ
Cos (α-β)=cos〖α cosβ 〗+Senα Senβ
Tan(α-β)=Tanα-Tan β⁄1+Tanα Tanβ
Resta de Ángulos
Sen θ/2=(±√(1-cosθ ))/2
Cos θ/2=±√((1+cosθ)/2)
Tan θ/2=1 (-cosθ)/senθ
Familia de Angulos medios
Sen θ=1/cscθ
Cosθ=1/secθ
Tanθ=1/Cot θ
Cotθ=1/tanθ
Sec θ=1/cosθ
Cscθ=1/sinθ
Reciprocas
1=sen^2θ+cos^2θ
1=sec^2θ-tan^2θ
1=csc^2θ-cot^2θ
Pitagoricas
Tan θ=(Sen θ)/cosθ
Cotθ=cosθ/sinθ
Cociente
Sen (2θ)=2senθ Cosθ
Cos(2θ)=cos^2θ-sⅇn^2 θ
Cos(2θ)=1-2sⅇn^2 θ
Cos(2θ)=2 cos^2θ-1
Familia de Ángulos Dobles