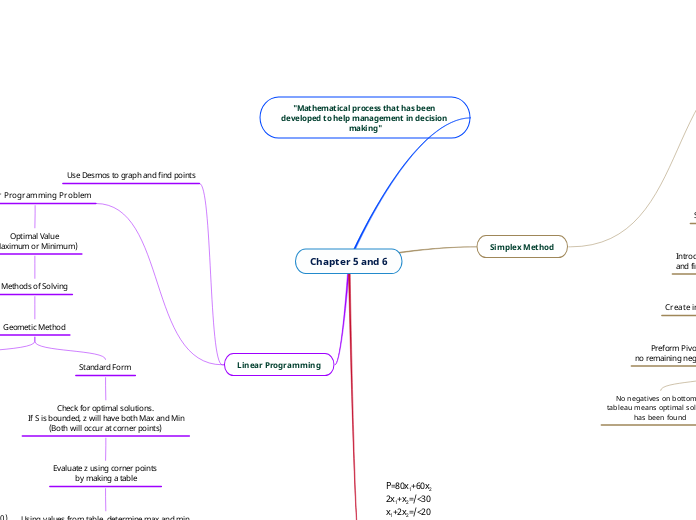
Chapter 5 and 6

Meer zoals dit

MAT.116 2.5-2.6

door David Kedrowski

INTRODUCTION TO OBJECT- ORIENTED PROGRAMMING (OOP)

door ALIYA NATASHA

Math Unit 1 Mind map

door Connor Gedney

where do people live?

door parmis esmaeili

Chapter 5 and 6

Shared Equations

Simplex Method

Standard Maximization Problem

2x1+x2+s1 =30 x1+2x2 +s2 =20 -80x1-60x2 +p=0

-2 - 1 1 0 0 30 l 30 -1 -2 0 1 0 20 l 20 -80-60 0 0 1 0 l 0

No Optimal Solution

2 1 1 0 0 30 l 30 1 2 0 1 0 20 l 20 -80-60 0 0 1 0 l 0

1 0 2/3 -1/3 0 l 131/3 0 1 -1/3 2/3 0 l 31/3 0 0 331/3 131/3 1 1266.7

P =1266.7 x1= 131/3 x2= 31/3

Introduce slack variables and find Initial System.

Create initial simplex tableau

Preform Pivot Operation until there are no remaining negatives in bottom row of tableau

No positives above dotted line in pivot column means there is no optimal solution

No negatives on bottom of tableau means optimal solution has been found

Linear Programming

Linear Programming Problem

Optimal Value (Maximum or Minimum)

Methods of Solving

Geometic Method

Standard Form

Check for optimal solutions. If S is bounded, z will have both Max and Min (Both will occur at corner points)

Evaluate z using corner points by making a table

Using values from table, determine max and min

P=80x1+60x2 2x1+x2=/<30 x1+2x2=/<20

2x1+x2 =30 x1+2x2 =20

x l y 80x1+60x2 0 l 0 0 Min:1200 0 l 20 1200 at (0,20) and (15,0) 10 l 10 1400 Max:1400 15 l 0 1200 at (10,10)

Use Desmos to graph and find points

"Mathematical process that has been developed to help management in decision making"