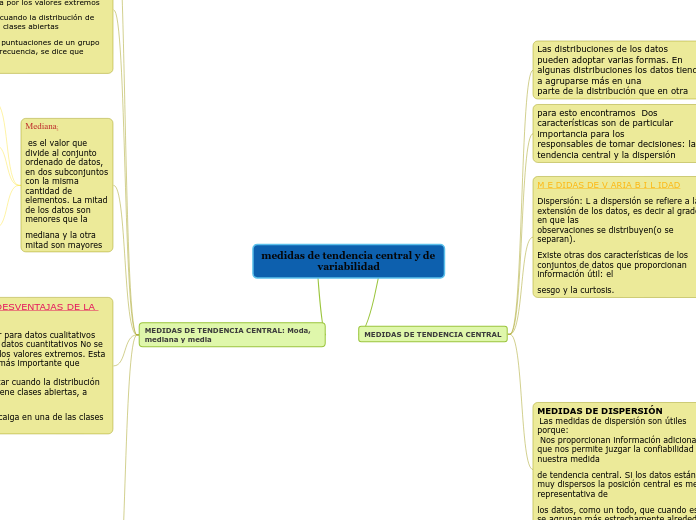
medidas de tendencia central y de variabilidad

Meer zoals dit

MEDIDAS DE LA VARIABILIDAD

door Jairo Florez

MEDIDAS DESCRIPTIVAS

door margoth peñaranda montes

Estructura de datos, mapa conceptual tablas hash

door Gianluca Casu

Desviación social.

door Whanda Isbet Lopez Cortez

medidas de tendencia central y de variabilidad

MEDIDAS DE TENDENCIA CENTRAL: Moda, mediana y media

Media o media aritmética: Es el promedio de los datos

VENTAJAS Y DESVENTAJAS DE LA MEDIA v Se trata de un concepto familiar e intuitivamente claro v Cada conjunto de datos tiene una media y es única v Es útil para llevar a cabo procedimientos estadísticos como la comparación de medias de varios conjuntos de datos. En estadística inferencial es la medida de tendencia central que tiene mejores propiedades

Cálculo de la media para datos agrupados Para calcular la media para datos agrupados, primero calculamos el punto medio de cada clase (marca de clase mi ). Después multiplicamos cada punto medio por la frecuencia absoluta de cada intervalo

Cálculo de la media para datos no agrupados Cuando calculamos la media de la población, dividimos por la cantidad de datos de la población N y cuando se calcula la media muestral por n

VENTAJAS Y DESVENTAJAS DE LA MEDIANA Se puede utilizar para datos cualitativos ordinales y para datos cuantitativos No se ve afectada por los valores extremos. Esta es la propiedad más importante que tiene. v Se puede utilizar cuando la distribución de frecuencias tiene clases abiertas, a menos que la mediana caiga en una de las clases abiertas

Mediana: es el valor que divide al conjunto ordenado de datos, en dos subconjuntos con la misma cantidad de elementos. La mitad de los datos son menores que la mediana y la otra mitad son mayores

Cálculo de la mediana para datos agrupados Si los datos están agrupados en una distribución de frecuencias, se selecciona el intervalo de clase que contiene a la mediana llamado clase mediana. Para ello, debemos determinar la frecuencia acumulada absoluta que contenga al elemento número n + 1\2

Número par de datos: Es el promedio entre los dos datos centrales

Número impar de datos: La mediana es el dato que está en la posición n +1\2

VENTAJAS Y DESVENTAJAS DE LA MODA Se puede utilizar para datos cualitativos nominales u ordinales y para datos cuantitativos No se ve afectada por los valores extremos Se puede utilizar cuando la distribución de frecuencias tenga clases abiertas Cuando todas las puntuaciones de un grupo tienen la misma frecuencia, se dice que no tiene moda

Moda: es el valor que más se repite en un conjunto de datos.

Cálculo de la moda para datos agrupados Si los datos están agrupados en una distribución de frecuencias, se selecciona el intervalo de clase que tiene mayor frecuencia llamado clase modal

MEDIDAS DE TENDENCIA CENTRAL

MEDIDAS DE DISPERSIÓN Las medidas de dispersión son útiles porque: Nos proporcionan información adicional que nos permite juzgar la confiabilidad de nuestra medida de tendencia central. Si los datos están muy dispersos la posición central es menos representativa de los datos, como un todo, que cuando estos se agrupan más estrechamente alrededor de la media.

Aplicación de la desviación estándar poblacional La desviación estándar nos permite determinar, con un buen grado de precisión, dónde están localizados los valores de una distribución de frecuencias con relación a la media.

El percentil p es un valor tal que por lo menos p porciento de las observaciones son menores o iguales que este valor y por lo menos (100-p) por ciento de las restantes son mayores o iguales que ese valor.

El coeficiente de variación es una medida relativa de dispersión que expresa a la desviación estándar como un porcentaje de la media

VARIANZA Y DESVIACIÓN ESTÁNDAR Las descripciones más comprensibles de la dispersión son aquellas que tratan con la desviación promedio con respecto a alguna medida de tendencia central. Veremos dos medidas que nos dan una distancia promedio con respecto a la media de la distribución: varianza y desviación estándar.

DESVIACIÓN ESTÁNDAR DE LA POBLACIÓN: Es la raíz cuadrada de la varianza

RANGO: Es la diferencia entre el mayor y el menor de los valores Observados

M E DIDAS DE V ARIA B I L IDAD Dispersión: L a dispersión se refiere a la extensión de los datos, es decir al grado en que las observaciones se distribuyen(o se separan). Existe otras dos características de los conjuntos de datos que proporcionan información útil: el sesgo y la curtosis.

curtosis: Nos da una idea de la agudeza (o lo plano) de la distribución de frecuencias. Una curva normal (es el patrón con el que se compara la curtosis de otras curvas) tiene curtosis 0. Esta curva se llama mesocúrtica

sesgo: Las curvas que representan un conjunto de datos pueden ser simétricas o sesgadas

para esto encontramos Dos características son de particular importancia para los responsables de tomar decisiones: la tendencia central y la dispersión

Las distribuciones de los datos pueden adoptar varias formas. En algunas distribuciones los datos tienden a agruparse más en una parte de la distribución que en otra