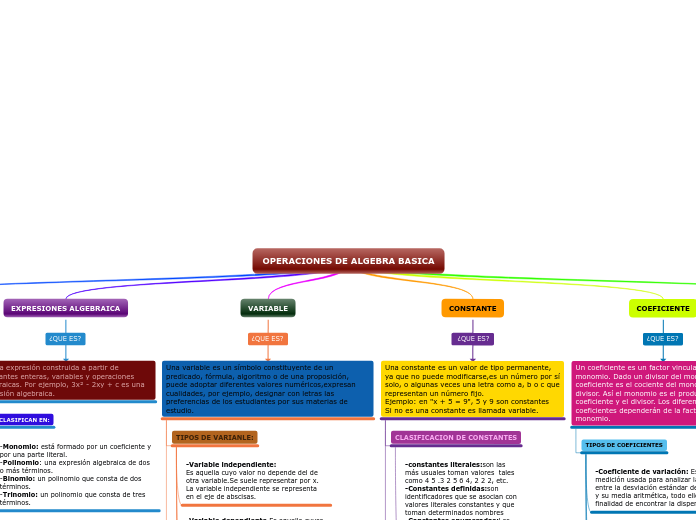
OPERACIONES DE ALGEBRA BASICA
OPERADORES
Un operador es un símbolo matemático que indica que debe ser llevada a cabo una operación especifica dada sobre un cierto número de operandos (número, función, vector, etc.)
Operadores logicos: proporcionan un resultado a partir de que se cumpla o no una cierta condición. Esto genera una serie de valores que, en los casos más sencillos, pueden ser parametrizados con los valores numéricos 0 y 1. La combinación de dos o más operadores lógicos conforma una función lógica.:
Los operadores de orden: establecen o verifican clasificaciones entre números (A < B, A > B, etc.) u otro tipo de valores (caracteres, cadenas, ...).
Todo tipo de dato susceptible de ser ordenado por cualquier criterio puede ser comparado con estos operadores;
A > B Devuelve V si A es estrictamente mayor que B y F en caso contrario
A < B Devuelve V si A es estrictamente menor que B y F en caso contrario
Operadores de condición:Relacionan un término A con otro B estableciendo su igualdad, jerarquía o cualquier otra relación posible, como ejemplos tenemos:
A = B establece que A es igual que B.
En este caso hay que distinguir entre operador = de asignación y el operador = de comparación. El primero toma el valor de B y se lo asigna a A; el segundo solamente compara los valores de A y B sin modificarlos y devuelve un valor lógico o de verdad verdadero si ambos valores son iguales o falso si dichos valores no son iguales.
COEFICIENTE
Un coeficiente es un factor vinculado a un monomio. Dado un divisor del monomio, el coeficiente es el cociente del monomio por el divisor. Así el monomio es el producto del coeficiente y el divisor. Los diferentes coeficientes dependerán de la factorización del monomio.
TIPOS DE COEFICIENTES
-Coeficiente de dilatación: se obtiene de la medición del cambio relativo de longitud o volumen que experimenta un cuerpo, sea que se encuentre en estado sólido, líquido o gaseoso, cuando es sometido a un cambio de temperatura, que podrá ser ascendente o descendente. En este sentido, el aumento de temperatura será proporcional a la dilatación, sea esta lineal, superficial o volumétrica.
-Coeficiente de fricción
En Física, el coeficiente de fricción, también llamado coeficiente de rozamiento, indica la oposición al deslizamiento que ofrecen las superficies de dos cuerpos en contacto.
-Coeficiente de correlación:Es una medida usada en Estadística para calcular el grado de relación lineal entre dos variables aleatorias, por ello, es también conocido como coeficiente de correlación lineal.
-Coeficiente de variación: Es una medición usada para analizar la relación entre la desviación estándar de una muestra y su media aritmética, todo ello con la finalidad de encontrar la dispersión relativa.
CONSTANTE
Una constante es un valor de tipo permanente, ya que no puede modificarse,es un número por sí solo, o algunas veces una letra como a, b o c que representan un número fijo.
Ejemplo: en "x + 5 = 9", 5 y 9 son constantes
Si no es una constante es llamada variable.
EJEMPLOS DE CONSTANTES
-El número de segundos en un minuto siempre son 60.
-El número de minutos en una hora siempre son 60.
-El número de horas en un día siempre son 24.
-El número de días en un año no bisiesto siempre son 365.
CLASIFICACION DE CONSTANTES
-constantes literales:son las más usuales toman valores tales como 4 5 .3 2 5 6 4, 2 2 2, etc.
-Constantes definidas:son identificadores que se asocian con valores literales constantes y que toman determinados nombres
-Constantes enumeradas:Las constantes enumeradas permiten asociar un identificador, tal como color , con una secuencia de otros nombres, tales como A z u l, Verde, R o j o y Amarillo.
-Cconstantes declaradas:
VARIABLE
Una variable es un símbolo constituyente de un predicado, fórmula, algoritmo o de una proposición, puede adoptar diferentes valores numéricos,expresan cualidades, por ejemplo, designar con letras las preferencias de los estudiantes por sus materias de estudio.
Ejemplos de variables independientes y dependientes
Desea comparar las marcas de toallas de papel, para ver cuál tiene el más líquido. La variable independiente en su experimento sería la marca de toalla de papel. La variable dependiente sería la cantidad de líquido absorbida por una toalla de papel.
TIPOS DE VARIANLE:
-Variable cualitativa:
Las variables cualitativas se refieren a características o cualidades que no pueden ser medidas con números.
-Variable cuantitativa:
Una variable cuantitativa es la que se expresa mediante un número, por tanto se pueden realizar operaciones aritméticas con ella.
-Variable dependiente.Es aquella cuyos valores dependen de los que tomen otra variable.
En una función se suele representar por y.
La variable dependiente se representa en el eje ordenadas.
La variable y está en función de la variable x.
-Variable independiente:
Es aquella cuyo valor no depende del de otra variable.Se suele representar por x.
La variable independiente se representa en el eje de abscisas.
EXPRESIONES ALGEBRAICA
Es una expresión construida a partir de constantes enteras, variables y operaciones algebraicas. Por ejemplo, 3x² - 2xy + c es una expresión algebraica.
EJEMPLOS:
El triple de un número menos dos: 3x-2
El doble de la suma de un número más dos: 2\left ( 3x-2 \right )
La quinta parte de un número al cubo: \cfrac{x^{3}}{5}
ELEMENTOS
Los elementos de una expresión algebraica son:
-Coeficiente: la parte numérica del término.
-Parte literal: las letras o variables de la expresión.
-Signo: el símbolo que indica si el término es positivo (+) o negativo (–).
-Exponente: los números que están arriba de las letras
SE CLASIFICAN EN:
-Monomio: está formado por un coeficiente y por una parte literal.
-Polinomio: una expresión algebraica de dos o más términos.
-Binomio: un polinomio que consta de dos términos.
-Trinomio: un polinomio que consta de tres términos.
COJUNTO DE NUMEROS
Son agrupaciones de números que guardan una serie de propiedades estructurales. Por ejemplo el sistema más usual en aritmética natural está formado por el conjunto de los números naturales, con la suma, la multiplicación y las relaciones usuales de orden aditivo.
N.ENTEROS
Es un elemento del conjunto numérico que contiene los números naturales, sus opuestos y el cero. Los enteros negativos, como −1 o −3, son menores que cero y todos los enteros positivos.
N.IRRACIONALES
Un número irracional es aquel que no puede ser obtenido mediante la fracción de dos números enteros. Conocemos algunos números irracionales como son la raíz de 2, el número pi, el número e, el número áureo y muchos otros.
N.RACIONALES
Se puede expresar como un número entero, un decimal exacto o un decimal periódico no todos los números decimales son exactos o periódicos
N.REALES
Los números reales se representan co la letra R y pueden ser expresados por un número entero (3, 28, 1568) o decimal (4,28; 289,6; 39985,4671),contiene todos los numeros que tienen jugar en la recta numerica.
N.NATURALES
Son los que desde el principio de los tiempos se han utilizado para contar.El conjunto de los números naturales se denota como N y se representan así: N:{1,2,3,4,5,6,....}