door Angelo Mustone 2 jaren geleden
381
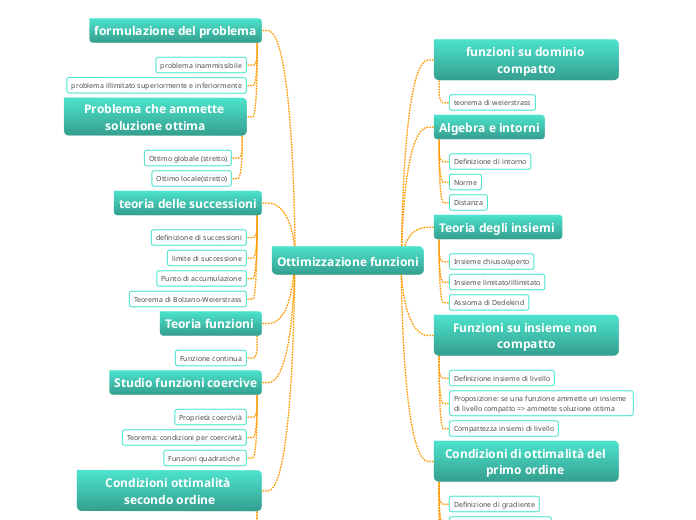
Ottimizzazione funzioni
Utilizzate questo modello a struttura radiale per organizzare le vostre idee, fare brainstorming, gestire progetti o compiti.
Parole chiave: diagrammi rapidi, mappa radiale, organizzare, concetto, compiti, idee, lista di cose da fare, lista di cose da fare, todolist, produttività, monocromo, luce, ciano.