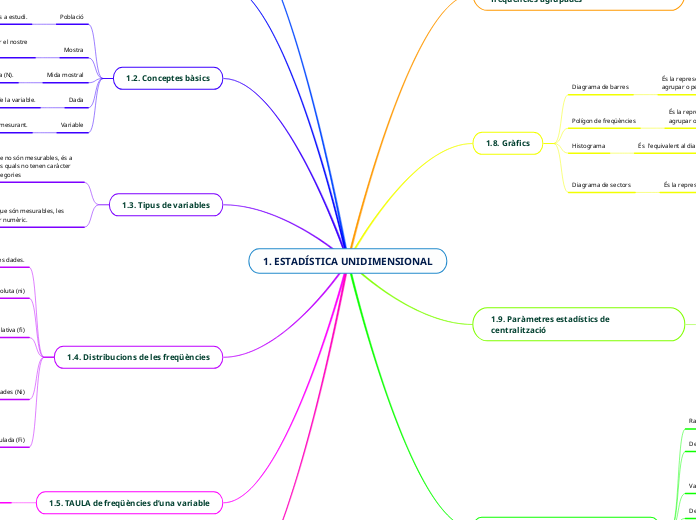
1. ESTADÍSTICA UNIDIMENSIONAL

1. Determinem el rang (o recorregut) de la variable

2. Nombre de classes

El nombre de classes en un histograma depèn de la mida de la mostra.

Per mostres de mida moderada (N < 50), es recomana utilitzar l'arrel quadrada d'n com a nombre de classes.

Per a mostres més grans s'utilitza la fórmula de Sturges (log(n) / log(2) + 1)

3. Determinem la amplitud dels intervals

És més còmode que l'amplitud de totes les classes sigui la mateixa

Si és així la fórmula és ai = a = Re/no intervals.

Prendrem com a regla general, fer que l'interval estigui tancat per l'esquerra i obert per la dreta (excepte el darrer interval).

Diagrama de barres

És la representació per al es variables quantitatives sense agrupar o per a variables qualitatives

A l'eix x afegim els valors de de la variable xi, i a l'eix y al freqüència absoluta o relativa

Polígon de freqüències

És la representació per a les varaibles quantitatives sense agrupar o per a variables qualitatives

Histograma

És l'equivalent al diagrama de barres per a dades agrupades

Diagrama de sectors

És la representació per a variables qualitatives

Es representen mitjançant cercles, i el sector és proporcional a la freqüència

Per a dades qualitatives, la distribució de freqüències resumeix la mostra. Per a dades quantitatives, s'utilitzen mesures descriptives numèriques per a resumir la informació de les dades.

Mitjana aritmètica

És el valor obtingut en sumar totes les dades i dividir-ho pel nombre total d'observacions. Cal tenir en compte que si hi ha dades repetides, s'han de considerar en el càlcul.

Mediana

La mediana és el valor que divideix un conjunt d'observacions a la meitat, deixant el 50% de les observacions a cada banda. És utilitzada per a descriure la posició central d'un conjunt de dades.

Si el nombre d'observacions és imparell, hi ha una dada central

Si el nombre d'observacions és parell, es prenen dues dades centrals i es calcula la mitjana entre elles

Moda

És aquell valor o interval més freqüent en la mostra

Quartils

Els quartils d'un conjunt ordenat de dades són els tres punts de tall que divideixen el conjunt de dades en quatre grups de la mateixa mida. Els quartils 25, 50 i 75 reben el nom de primer quartil, segon quartil i tercer quartil. El segon quartil coincidirà sempre amb la mediana.

Rang o recorregut

Desviacions respecte la mitjana (Dm)

És la diferència entre una dada (xi) i la seva mitjana (x)

Fórmula: Valor absolut de xi-x

Variància (S2)

La variança mesura la dispersió de les dades respecte a la mitjana. Si les dades estan molt separades de la mitjana, hi haurà una variança elevada.

Fórmula: (Dm) elevat al quadrat *ni / n

Desviació típica (S)

És l'arrel quadrada de la variància

Rang interquartílic

La mesura de dispersió d'una distribució es calcula restant el primer quartil al tercer quartil. Aquesta diferència reflecteix la distància entre els valors que divideixen la distribució en quatre parts iguals.

Coeficient de variació (Cv)

És una mesura que compara la dispersió de dues seqüències de dades expressades en diferents unitats.  Això ens permet determinar quina seqüència té una major dispersió. És una eina útil per comparar dades amb diferents unitats i proporciona una mesura relativa de la dispersió.

Fórmula: Cv = S/x

L'estadística descriptiva és una branca de l'estadística que es dedica a l'organització, resum i primera descripció de les dades.

Població

Conjunt d’individus o ens subjectes a estudi.

Mostra

Nombre de dades que prenem de la població per fer el nostre estudi.

Mida mostral

Nombre d'observacions a la mostra (N).

Dada

Cada valor observat de la variable.

Variable

Característica que estem mesurant.

Variables qualitatives: Aquelles que no són mesurables, és a dir aquelles les observacions de les quals no tenen caràcter numèric. Expressen qualitats o categories

Nominals: Tenen qualitat que no són ordenables.

Ordinals:Tenen qualitats que poden ser ordenades.

Variables quantitatives: Aquelles que són mesurables, les seves observacions tenen caràcter numèric.

Discretes: Tenen valors numèrics fixes.

Continues:Tenen valors en intervals numèrics.

Les freqüències són utilitzades per a organitzar les dades.

Freqüència absoluta (ni)

És el nombre de vegades que es repeteix un valor específic en una mostra de la variable.

Propietat: La suma de totes les freqüències absolutes és igual al tamany de la mostra.

Freqüència relativa (fi)

És igual a la freqüència absoluta dividida pel nombre total de dades, és dir per la mida mostral.

Fórmula: ni/N=fi

Propietat: La suma de totes les freqüències relatives és igual a 1

Freqüències acumulades (Ni)

Ens indica la quantitat de dades que són iguals o inferiors a un valor específic.

S'ha de sumar les freqüències absolutes dels elements anteriors a aquest.

Propietat: La freqüència acumulada final és igual al nombre total de dades en la mostra.

Freqüència relativa acumulada (Fi)

Es calcula dividint cada freqüència acumulada pel total de dades.

Fórmula: Ni/N

En un estudi estadístic, després de recollir les dades, es presenten de manera clara i comprensible mitjançant taules de freqüències. Això facilita la visualització i l'anàlisi dels valors recopilats.

Per a variables contínues amb molts valors, pot ser incòmode de llegir. Agrupar-los en intervals o intervals de classe simplifica la taula resultant, tot i que implica una pèrdua de precisió en els resultats.

Agrupar en intervals de classe és el procés de dividir les dades en intervals de nombres petits que compleixen les següents condicions:

Evita la superposició i l'ambigüitat entre les classes per a una observació concreta.

Cobreixin tot el rang de valors que tenim a la mostra.

S'anomenen:

A les fronteres de l'interval, límits inferior i superior de classe

li, Li respectivament.

Marca de classe (ci) al punt mitjà de l'interval, és a dir, a la mitjana aritmètica

Recorregut o rang (R) és la diferència entre l'extrem superior i inferior

R = Li - li

Al nombre d'observacions d'una classe se'n diu freqüència de classe (ni)

Si dividim aquesta freqüència pel nombre total d'observacions, s'obté la freqüència relativa de classe (fi).