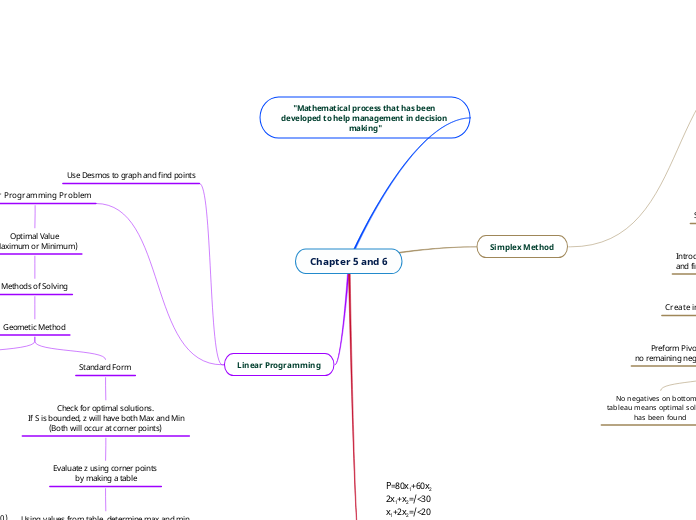
Chapter 5 and 6
"Mathematical process that has been developed to help management in decision making"
Linear Programming
Use Desmos to graph and find points
Linear Programming Problem
Optimal Value
(Maximum or Minimum)
Methods of Solving
Geometic Method
P=80x1+60x2
2x1+x2=/<30
x1+2x2=/<20
2x1+x2 =30
x1+2x2 =20
x l y 80x1+60x2
0 l 0 0 Min:1200
0 l 20 1200 at (0,20) and (15,0)
10 l 10 1400 Max:1400
15 l 0 1200 at (10,10)
Standard Form
Check for optimal solutions.
If S is bounded, z will have both Max and Min
(Both will occur at corner points)
Evaluate z using corner points
by making a table
Using values from table, determine max and min
Simplex Method
Standard Maximization Problem
Optimal Value
(Maximum or Minimum)
Methods of Solving
Simplex Method
Standard Form
Introduce slack variables
and find Initial System.
Create initial simplex tableau
Preform Pivot Operation until there are
no remaining negatives in bottom row of tableau
No negatives on bottom of
tableau means optimal solution
has been found
No positives above dotted line
in pivot column means there is
no optimal solution
P=80x1+60x2
2x1+x2=/<30
x1+2x2=/<20
2x1+x2+s1 =30
x1+2x2 +s2 =20
-80x1-60x2 +p=0
2 1 1 0 0 30 l 30
1 2 0 1 0 20 l 20
-80-60 0 0 1 0 l 0
1 0 2/3 -1/3 0 l 131/3
0 1 -1/3 2/3 0 l 31/3
0 0 331/3 131/3 1 1266.7
P =1266.7
x1= 131/3
x2= 31/3
-2 - 1 1 0 0 30 l 30
-1 -2 0 1 0 20 l 20
-80-60 0 0 1 0 l 0
No Optimal
Solution
Shared Equations
P=80x1+60x2
2x1+x2=/<30
x1+2x2=/<20