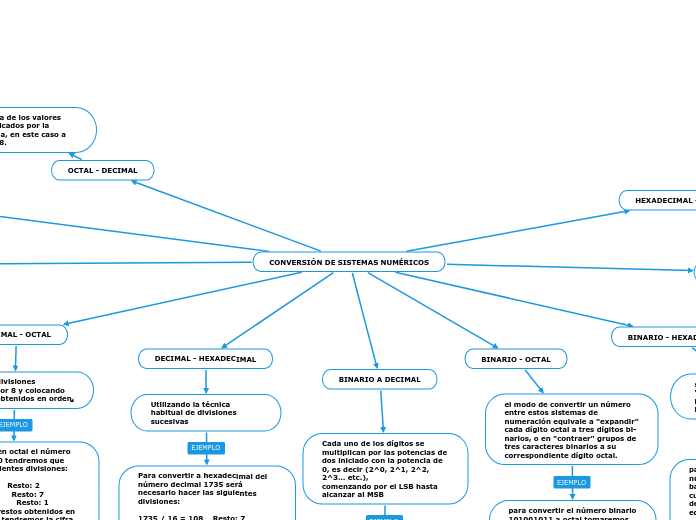
CONVERSIÓN DE SISTEMAS NUMÉRICOS

DECIMAL - BINARIO

Divisiones sucesivas por 2 y escribir los restos obtenidos en cada división en orden inverso al que han sido obtenidos

para convertir al sistema binario el número decimal 77 haremos una serie de divisiones que arrojarán los restos siguientes:
77 / 2 = 38 Resto: 1
38 / 2 = 19 Resto: 0
19 / 2 = 9 Resto: 1
9 / 2 = 4 Resto: 1
4 / 2 = 2 Resto: 0
2 / 2 = 1 Resto: 0
1 / 2 = 0 Resto: 1
tomando los restos en orden inverso obtenemos la cifra binaria:
Decimal 77 = Binario 1001101

BINARIO A DECIMAL

Cada uno de los dígitos se
multiplican por las potencias de dos iniciado con la potencia de 0, es decir (2^0, 2^1, 2^2, 2^3… etc.),
comenzando por el LSB hasta alcanzar al MSB

vamos a pasar el número binario 100110 a decimal: 1=1·2^5=32
0=1·2^4=0
0=1·2^3=0
1=1·2^2=4
1=1·2^1=2
0=1·2^0=0 El resultado es 32 +4 +4 = 38

^

HEXADECIMAL - BINARIO

La conversión se obtiene al
reemplazar cada cifra
hexadecimal por su equivalente
binario (formado de 4 bits)

A esta agrupación de 4 bits se le
denomina Nibble, por lo que un
byte en hexadecimal se
compone de 2 nibbles.

el número hexadecimal 1F6 hallaremos en la tabla las siguientes equivalencias:

1 = 0001
F = 1111
6 = 0110

y, por lo tanto el número hexadecimal 1F6 = al binario 000111110110

BINARIO - HEXADECIMAL

se realiza "expandiendo" o "con­trayendo" cada dígito hexadecimal a cuatro dígitos binarios.

para expresar en hexadecimal el número binario 101001110011 bastará con tomar grupos de cuatro bits, empezando por la derecha, y reemplazarlos por su equivalente hexadecimal:

1010 = A
0111 = 7
0011 = 3

por tanto el número binario 101001110011 = al hexadecimal A73

En caso de que los dígitos binarios no formen grupos completos de cuatro dígitos, se deben añadir ceros a la izquierda hasta completar el último grupo

101110 = 00101110 = 2E en hexadecimal

DECIMAL - OCTAL

Mediante divisiones sucesivas por 8 y colocando los restos obtenidos en orden inverso.^

Para escribir en octal el número decimal 12210 tendremos que hacer las siguientes divisiones:

122 / 8 = 15 Resto: 2
15 / 8 = 1 Resto: 7
1 / 8 = 0 Resto: 1
Tomando los restos obtenidos en orden inverso tendremos la cifra octal:

Decimal 122 = Octal 172

DECIMAL - HEXADECIMAL

Utilizando la técnica habitual de divisiones sucesivas

Para convertir a hexadecimal del número decimal 1735 será necesario hacer las siguientes divisiones:

1735 / 16 = 108 Resto: 7
108 / 16 = 6 Resto: C es decir, 12 en decimal
6 / 16 = 0 Resto: 6

De ahí que, tomando los restos en orden inverso, resolvemos el número en hexadecimal:

decimal 1735 = hexadecimal 6C7

BINARIO - OCTAL

el modo de convertir un número entre estos sistemas de numeración equivale a "expandir" cada dígito octal a tres dígitos bi­narios, o en "contraer" grupos de tres caracteres binarios a su correspondiente dígito octal.

para convertir el número binario 101001011 a octal tomaremos grupos de tres bits y los sustituiremos por su equivalente octal:

101 = 5 octal
001 = 1 octal
011 = 3 octal
y, de ese modo el número binario 101001011 = octal 513

OCTAL - BINARIO

reemplazando cada dígito octal por los tres bits equivalentes^

para convertir el número octal 750 a binario, tomaremos el equivalente binario de cada uno de sus dígitos:

7 octal = 111
5 octal = 101
0 octal = 000

y, por tanto el número octal 750 = 111101000 binario

OCTAL - DECIMAL

La suma de los valores multiplicados por la potencia, en este caso a base a 8.

vamos a pasar el número octal 356,243 a decimal:

3 = 3·8^2=192
5 = 5·8^1=40
6= 6·2^0=6
,
2 = 2·8^-1=0,25
4= 4·8^-2=0,0625
3= 3·8^-3=0,005893

El resultado es: 192 + 40 + 6 , 0,25 + 0,0625 + 0,005893 = 238,318

HEXADECIMAL - DECIMAL

La suma de los valores multiplicados por la potencia, en este caso a base a 16

Vamos a pasar el número hexadecimal EE,51E a decimal:
E= E·16^1=224
E= E·16^0=14
,
5= 5·16^-1=0,3125
1=1·16^-2=0,003906
E= E·16^-3=0,00341
El resultado es: 224 + 14 , 0,3125 + 0,003906 + 0,00341 = 238,3198…