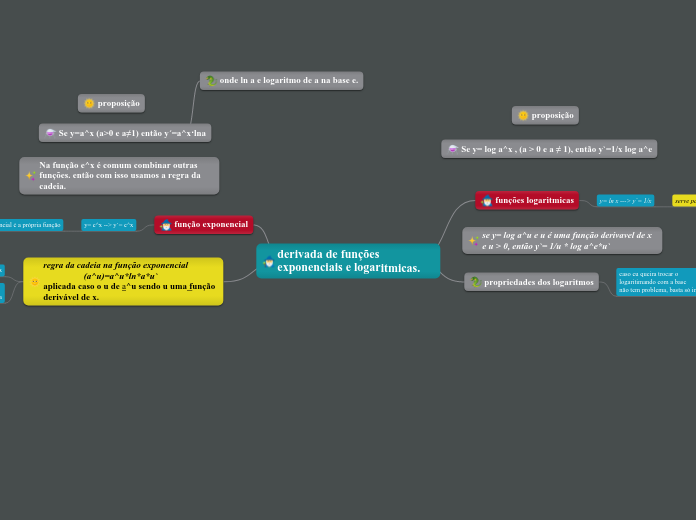
derivada de funções exponenciais e logaritmicas.
função exponencial
y= e^x --> y`= e^x
a derivada da função exponencial é a própria função
regra da cadeia na função exponencial
(a^u)=a^u*ln*a*u`
aplicada caso o u de a^u sendo u uma função derivável de x.
y=3^x²-5x
derivada usando a rega da cadeia
y`=3^x²-5x*ln*(2x-5)
com o caso mais usado sendo:
(e^u)= e^u*u` pela regra da cadeia
funções logaritmicas
y= ln x ---> y`= 1/x
serve para a base é e
propriedades dos logaritmos
caso eu queira trocar o
logaritimando com a base
não tem problema, basta sò inverter
log a^b = 1/log b^a
serve para resolver problema como:
y`=1/x log a^e = 1/x*1/log e^a