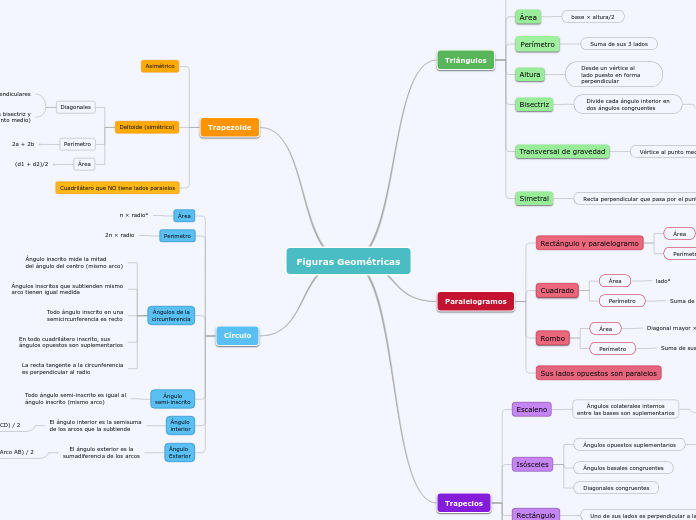
Figuras Geométricas
Triángulos
Teorema de Pitágoras
Aplicación en triángulos rectángulos
(tiene un ángulo de 90°)
En todo cuadrado
d²= a² + a²
d = a√2
Triángulo equilátero
h²= a² + (a/2)²
h = (a/2)√3
hipotenusa² = cateto² + cateto²
Ternas notables o trios pitagóricos
Catetos: 3-4 Hipotenusa: 5
Catetos: 5-12 Hipotenusa: 13
Catetos: 8-15 Hipotenusa: 17
Área
base × altura/2
Perímetro
Suma de sus 3 lados
Altura
Desde un vértice al lado puesto en forma perpendicular
Bisectriz
Divide cada ángulo interior en
dos ángulos congruentes
Incentro: intersección de las bisectrices
Transversal de gravedad
Vértice al punto medio del lado puesto
Centro de gravedad (G): intersección
de las transversales de gravedad
Si es triángulo rectángulo en C
CD es transversal de gravedad
D es punto medio de AB
AD=DB=CD
Simetral
Recta perpendicular que pasa por el punto medio de cada lado
Circuncentro: intersección de simetrales
Paralelogramos
Rectángulo y paralelogramo
Área
base × altura
Perímetro
Suma de sus 4 lados
Cuadrado
Área
lado²
Perímetro
Suma de sus 4 lados
Rombo
Área
Diagonal mayor × Diagonal menor / 2
Perímetro
Suma de sus lados
Sus lados opuestos son paralelos
Trapecios
Escaleno
Ángulos colaterales internos
entre las bases son suplementarios
Alfa + Gama = 180º
Beta + Delta = 180º
Isósceles
Ángulos opuestos suplementarios
Alfa + Beta = 180º
Ángulos basales congruentes
Diagonales congruentes
Rectángulo
Uno de sus lados es perpendicular a las bases
Alfa + Beta = 180º
Área
((B + b)/2) x h
Perímetro
a + b + c + d
Cuadrilátero que tiene sólo un
par de lados paralelos
Trapezoide
Asimétrico
Deltoide (simétrico)
Diagonales
Perpendiculares
La más larga es bisectriz y
simetral de la otra (punto medio)
Perímetro
2a + 2b
Área
(d1 + d2)/2
Cuadrilátero que NO tiene lados paralelos
Círculo
Área
π × radio²
Perimetro
2π × radio
Ángulos de la
circunferencia
Ángulo inscrito mide la mitad
del ángulo del centro (mismo arco)
Ángulos inscritos que subtienden mismo
arco tienen igual medida
Todo ángulo inscrito en una
semicircunferencia es recto
En todo cuadrilátero inscrito, sus
ángulos opuestos son suplementarios
La recta tangente a la circunferencia
es perpendicular al radio
Ángulo
semi-inscrito
Todo ángulo semi-inscrito es igual al
ángulo inscrito (mismo arco)
Ángulo
interior
El ángulo interior es la semisuma
de los arcos que la subtiende
(Arco AB + Arco CD) / 2
Ángulo
Exterior
El ángulo exterior es la
sumadiferencia de los arcos
(Arco CD - Arco AB) / 2