Fundamentals of Geometry for Elementary School Teachers
Angles
Regular Polygon Angles
Interior Angle
(n-2)180/n OR 180-(360/n)
Central Angle
360/n
Exterior Angle
360/n
Describing Angles in Relation to Their Degree

Zero

Parallel Lines

Acute

Right
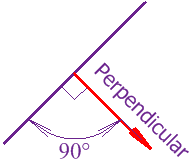
Perpendicular Lines
Negative Reciprocal

Obtuse
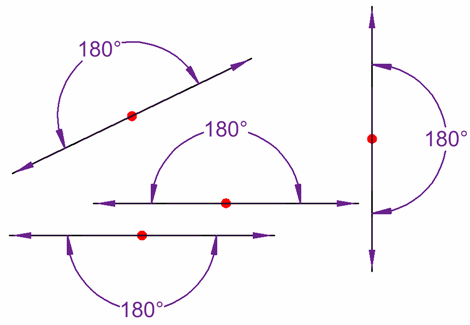
Straight
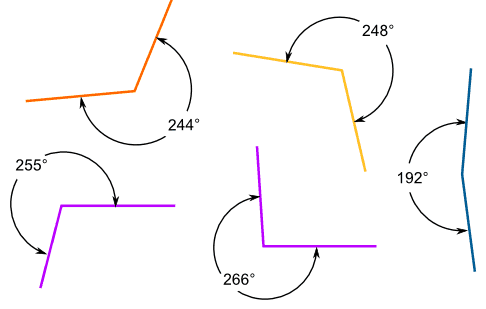
Reflex
Transformations

Translation
slide

Rotation
turn from a given point
COUNTERCLOCKWISE

Reflection
flip

Glide
reflection (glide-flip)
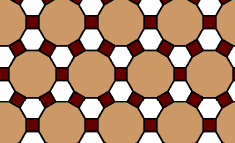
Only 3 Regular Tilings:

Triangle

Square

Hexagon

Same pattern at every vertex

Using more then one regular polygon to make 360 degrees at the vertex.
Shapes
Regular Polygon
When a polygon has an odd number of sides....
If it is equilagular it has to be equilateral aswell,
and vise versa.
Why?
Because it has no parallel sides.
Equiangluar Polygon
Equilateral Polygon

Congruent
Concave
Convex
Self-itersecting Polygon
Lattice Polygon
Formula for the Sum of the Angles Within ANY Polygon
Names of Polygons

Triangles (trigon)
The sum of all of the angles within a triangle is 180 degrees.
Types of Triangles
Acute
Obtuse
Right
Equilateral
Isoceles
Scalene
Quadrilaterals (tetragon)

Trapezoid

Isosceles Trapezoid
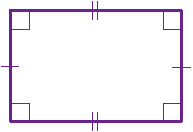
Rectangle

Square
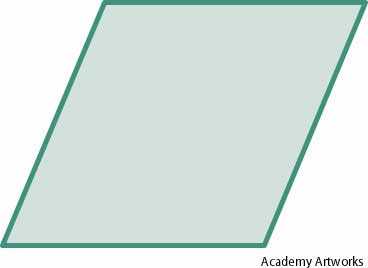
Rhombus

Parallelograms

Kite
Pentagon
Hexagon
Heptagon
More info...
Names of Different Polyhedras

Pyramid

Apex
4 or more faces (n + 1)= faces
Determining Their Names
Always Convex

Prism
Convex or Concave
Planes
Lateral
Determining Their Names
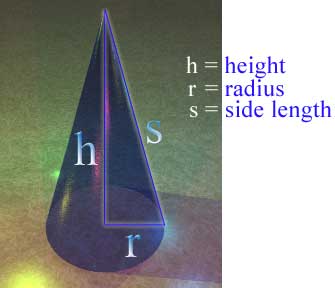
Cones
Closed, "Curved" base
Determining Their Names
Cylinders
Two closed, parallel, curved bases
Determining Their Names

Line Segment

Vertex

Ray