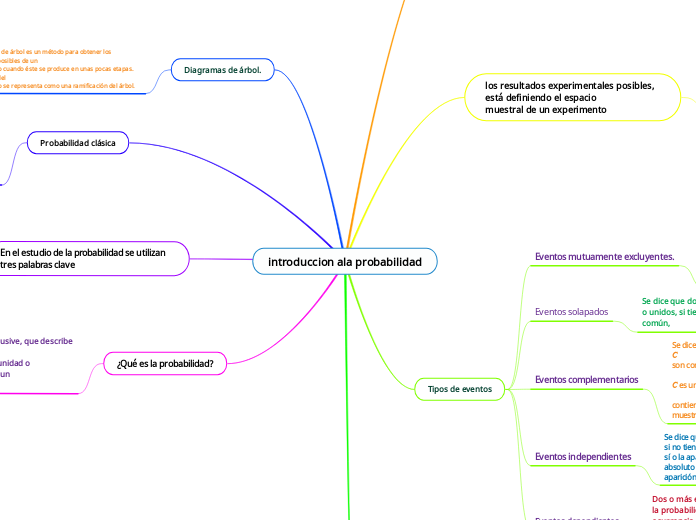
introduccion ala probabilidad
Axioma de probabilidad.
El cálculo de probabilidades tiene tres axiomas o postulados del evento
probabilístico:
Axioma 1 de positividad
: la probabilidad de un evento es no negativo: es cero
o positivo; es decir P(E) ≥ 0.
Axioma 2 de certidumbre:
a probabilidad del espacio muestral es 1; es decir,
P(S) = 1. Entonces tomando los pos axiomas se puede afirmar que la
probabilidad de cualquier evento E varía entre 0 y 1; es decir 0≤P(E)≤1.
Axioma 3 de las uniones:
probabilidad de un evento compuesto E es igual a
la suma de las probabilidades de los eventos simples de los cuales E es
compuesto; es decir Ei es un evento compuesto de los eventos simples e1, e2,
e3,…, ek; entonces P(E) = P(e1) + P(e2) + P(e3)+…+ P(ek).
los resultados experimentales posibles, está definiendo el espacio
muestral de un experimento
ESPACIO MUESTRAL
Es espacio muestral de un experimento es el
conjunto de todos los resultados experimentales. Normalmente se
denota por S.
Tipos de eventos
Eventos mutuamente excluyentes.
Decimos que dos eventos A y B son mutuamente excluyentes si A y B no contienen
puntos muestrales en común, es decir su intersección es el conjunto vacío: 𝐴 ∩ 𝐵 = ∅
Eventos solapados
Se dice que dos eventos A y B, son solapados o unidos, si tienen puntos muéstrales en
común,
Eventos complementarios
Se dice que los eventos 𝐴 y 𝐴
𝐶
son complementarios si 𝐴
𝐶 es un subconjunto que
contiene todos los puntos muestrales del espacio muestral que no están en 𝐴.
Eventos independientes
Se dice que dos o más eventos son independientes si no tienen relación alguna entre
sí o la aparición de cualquiera de ellos no afecta en absoluto la probabilidad de
aparición del otro u otros
Eventos dependientes
Dos o más eventos son dependientes cuando la probabilidad de ocurrencia o no
ocurrencia de uno de esos eventos, afecta la probabilidad de otros eventos, en otras
pruebas
La probabilidad constituye parte importante de nuestra vida cotidiana. En la toma de
decisiones personales y administrativas, nos enfrentamos a la incertidumbre y utilizamos
la teoría de la probabilidad, admitamos o no el uso de algo tan complejo. Cuando
escuchamos una predicción de un 70% de posibilidades de lluvia
Diagramas de árbol.
El diagrama de árbol es un método para obtener los resultados posibles de un
experimento cuando éste se produce en unas pocas etapas. Cada paso del
experimento se representa como una ramificación del árbol.
Probabilidad clásica
parte del supuesto de que los resultados de un experimento
son igualmente posibles. De acuerdo con el punto de vista clásico, la probabilidad de
un evento que se está llevando a cabo se calcula dividiendo el número de resultados
favorables entre el número de posibles resultados:
En el estudio de la probabilidad se utilizan tres palabras clave
experimento
Proceso que induce a que ocurra una y sólo una de
varias posibles observaciones.
resultado
consecuencia obtenida al realizar un experimento
evento
Conjunto de uno o más resultados de un experimento
¿Qué es la probabilidad?
Valor entre cero y uno, inclusive, que describe la
posibilidad relativa (oportunidad o casualidad) de que ocurra un
evento.