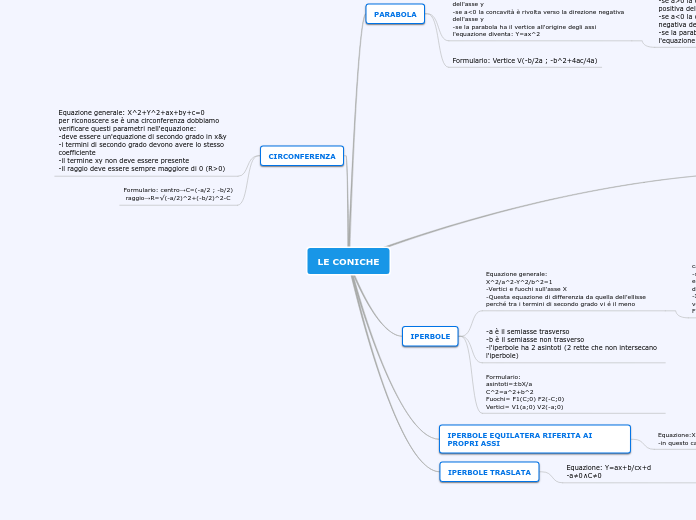
LE CONICHE

Equazione generale:
Y=ax^2+bx+c
questa parabola ha l'asse di simmetria parallelo all'asse y
-se a>0 la concavità è rivolta verso la direzione positiva dell'asse y
-se a<0 la concavità è rivolta verso la direzione negativa dell'asse y
-se la parabola ha il vertice all'origine degli assi l'equazione diventa: Y=ax^2

Eccezioni:
X=ay^2+by^2+c
questa equazione mi dice che la parabo!a ha asse di simmetria parallelo all'asse dellle x
-se a>0 la concavità è rivolta verso la direzione positiva dell'asse x
-se a<0 la concavità è rivolta verso !a direzione negativa dell'asse delle x -se la parabola ha il vertice all'origine degli assi l'equazione diventa: X=ay^2

Formulario: Vertice V(-b/2a ; -b^2+4ac/4a)

Equazione generale:
X^2/a^2+Y^2/b^2=1
-se l'equazione non è ridotta in forma normale ci si può confondere con la circonferenza ma per non cadere in quest'errore basterà verificare che il coefficiente dei termini di secondo grado non sono uguali.

- a&b sono i semiassi

Vertici: (0;a)(0;b)(0;-a)(0;-b)

-se a>b i fuochi si trovano sull'asse X C^2=a^2-b^2 F1(-C;0) F2(C;0) -se a<b i fuochi si trovano sull'asse Y C^2=b^2-a^2 F1(0;-C) F2(0;C)

Equazione generale: X^2/a^2-Y^2/b^2=1 -Vertici e fuochi sull'asse X -Questa equazione di differenzia da quella dell'ellisse perché tra i termini di secondo grado vi é il meno

casi particolari: -se i semiassi sono uguali a=b l'iperbole si dice equilatera e l'equazione diventa X^2-Y^2=a^2 e gli asintoti diventano Y=±X -X^2/a^2-Y^2/b^2=-1 vertici e fuochi sull'asse Y V1(0;b) V2(0;-b) F1(0;C) F2(0;-c)

-a è il semiasse trasverso -b è il semiasse non trasverso -l'iperbole ha 2 asintoti (2 rette che non intersecano l'iperbole)

Formulario: asintoti=±bX/a C^2=a^2+b^2 Fuochi= F1(C;0) F2(-C;0) Vertici= V1(a;0) V2(-a;0)

Equazione:X^2-Y^2=±a^2 -in questo caso l'equazione degli asintoti sarà X*Y=K

Equazione: Y=ax+b/cx+d -a≠0∧C≠0

Asintoti X=-d/c Y=a/c C(-d/c ; Y=a/c )

Equazione generale: X^2+Y^2+ax+by+c=0
per riconoscere se è una circonferenza dobbiamo verificare questi parametri nell'equazione:
-deve essere un'equazione di secondo grado in x&y
-i termini di secondo grado devono avere lo stesso coefficiente
-il termine xy non deve essere presente
-il raggio deve essere sempre maggiore di 0 (R>0)

Formulario: centro→C=(-a/2 ; -b/2)
raggio→R=√(-a/2)^2+(-b/2)^2-C