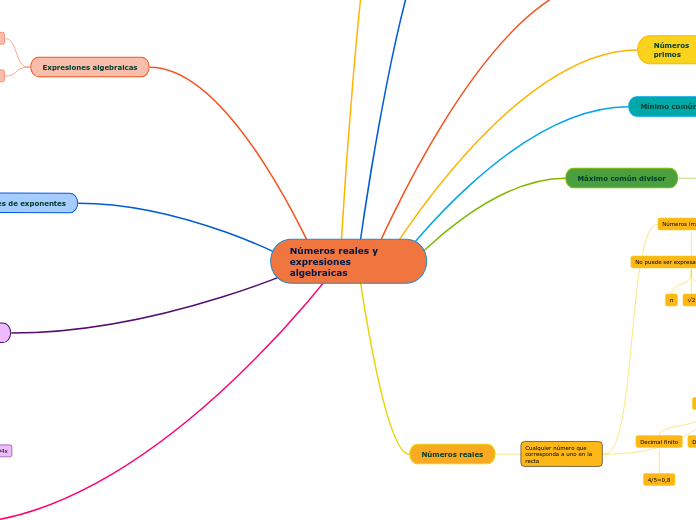
Números reales y expresiones algebraicas
Jerarquía de las operaciones
1.Signos de agrupación
Resolver los paréntesis
[...] (...)
2.Potenciación (26)
Raíz (√6)
Factorial (n!=n (n-1)(n-2)...)
3.Multiplicación y división
5x8=40
45/5=9
4.Suma y resta
28+52=80
340-50=290
Divisibilidad
Al dividirlo, esta nos tiene que dar un número entero
45/3=15
Números primos
Divisibles por ellos y por otro número entero
2,3,5,7,11
Mínimo común múltiplo
Múltiplo mas pequeño que tienen en común
(2,4,8)=24
Máximo común divisor
Divisor mas grande que tienen en común
(5,7,10)=1
Números reales
Cualquier número que corresponda a uno en la recta
Números irracionales
No puede ser expresado de la forma a/b
π
√2
e
Números racionales
Aquel que se representa de la forma
a/b
Decimal finito
4/5=0,8
Decimal infinito periodico
2/3=0,6
Operaciones combinadas de fracciones
Multiplicación
a/b X a/b = a X a/b X b
Se multiplican
12/25 X 10/9 X 4/21
Numeradores
12X10X4
32
Denominadores
25X9X21
215
División
a/b X a/b = a X b/ a X b
5/2÷ 3/4
5X4
3X2
Suma
Se saca el MCM
Se multiplica el numerador
Resta
Se saca el MCM
Se multiplica el numerador
Números enteros
Contiene a los números naturales
Se representan en una recta
Positivos
1,2,3,4,5
Negativos
-1,-2,-3,-4,-5
Expresiones algebraicas
Multiplicación
(x-4)2
(x-4)(x-4)
(x.x)+(x.(-4))+(-4.x)(-4.-4)
x2-4x-4x+16
x2-8x+16
División
4x3y2 - 5x2y3 + 3xy4 / 2x2y3
4x3y2/ 2x2y3
2xy-1
-5x2y3 / 2x2y3
-5/2 x0y0
2x/y -5/2 +3y/2x
+3x3y4 / 2x2y3
3/2 x-1 y
Leyes de exponentes
Ley de signos
(+)(+)= +
(-)(-)= +
(+)(-)= -
Propiedades de la potencia
Xn x Xm= Xn+m (exponentes)
Xn/Xm=Xn-m
Xn x Yn=(xy)n
Xn/Yn=(x/y)n
X0=1
X-n=1/xn
Expresiones algebraicas
Suma y resta de polinomios
Suma
3x+24x+24x=51 x
Resta
-81x-8x-5x=94x
Conjuntos e intervalos
Conjuntos
Números naturales (N)
{1,2,3,4,5...}
Números fraccionarios (Q+)
{1/2, 3/4, 6/7 }
Números enteros (Z)
{-3,-3,1,5 }
Números racionales (Q)
{-1/2, 0, 1/4 }
Números irracionales (I)
{1,4142135}
Números reales (R)
{ -10,-1-3/4,√2}
Números imaginarios (i)
{√-1}
Intervalos de ℝ
(a,b)
(3,8)
Ninguno pertenece
[a,b]
[3,8]
Ambos pertenecen
(a,b]
(3,8]
El 3 no pertenece, el 8 si
[a,b)
[3,8)
El 3 pertenece, el 8 no
(-∞,a)
(-∞,8)
Ninguno pertenecen
(-∞,a]
(-∞,8]
El menos infinito no pertenece, el 8 si
(b, +∞)
(b, +∞)
Ninguno pertenece
[b,+∞)
[b,+∞)
La b pertenece, el mas infinito no