Parabola y Circunferencia
Forma canonica
(x-h)2 + (y-K)2 = r2
Centro (h, k)
Centro: el centro C es el punto interior que está a una distancia r de todos los puntos de la circunferencia

Corte al cono.
Al tomar un plano paralelo a la base del cono y realizar el corte es como se obtiene una circunferencia.

Los principales elementos de la circunferencia son:
Radio: es el segmento r que une el centro (C) de la circunferencia con cualquiera de sus puntos.
Diámetro: segmento D que une dos puntos de la circunferencia y que pasa por el centro (C). Su longitud es el doble que la del radio.
Cuerda: es un segmento K que une dos puntos de la circunferencia sin necesidad de pasar por el centro.
Arco: es la parte de la circunferencia que queda entre los dos extremos de una cuerda (a).
Ángulo central: es el ángulo entre dos segmentos que van del centro a dos puntos de la circunferencia (α)

Corte al cono.
Al tomar un plano paralelo a la generatriz del cono y realizar el corte es como se obtiene una parabola.
Una parábola es el lugar geométrico de los puntos del plano que equidistante de un punto fijo, llamado foco y de una recta fija del mismo plano llamada directriz.
Forma canonica.
(x-h)2 +/- 4p (y-k)2
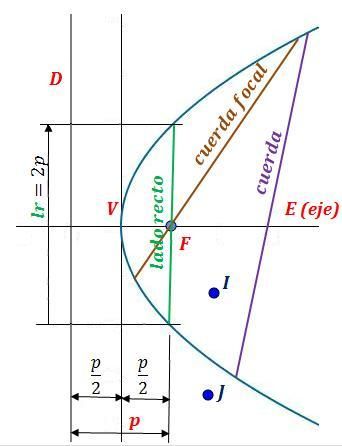
Los elementos de la parabola son:
Foco: el foco F es el punto fijo. Los puntos de la parábola equidistan del foco y la directriz.
Directriz: es la recta fija D. Los puntos de la parábola equidistan de la directriz y el foco.
Radio vector: es el segmento R que une el foco con cada uno de los puntos de la parábola. Es igual al segmento perpendicular a la directriz desde el punto correspondiente.
Eje: es la recta E perpendicular a la directriz que pasa por el foco y el vértice. Es el eje de simetría de la parábola.
Parámetro: es el vector p, que va desde el foco al punto más próximo de la directriz.
Vértice: es el punto V de la intersección del eje y la parábola.
Distancia focal: distancia entre el foco F y el vértice V. Es igual a p/2.
Puntos interiores y exteriores: la parábola divide el plano en dos regiones. Los puntos que están en la región del foco se llaman puntos interiores (I), mientras que los otros son los exteriores (J).
Cuerda: segmento que une dos puntos cualesquiera de la parábola.
Cuerda focal: una cuerda que pasa por el foco F.
Lado recto: Cuerda focal paralela a la directriz D y, por tanto, perpendicular al eje E. Su longitud es dos veces el parámetro (2p, pues se ven en la figura dos cuadrados unidos iguales de lado p).
