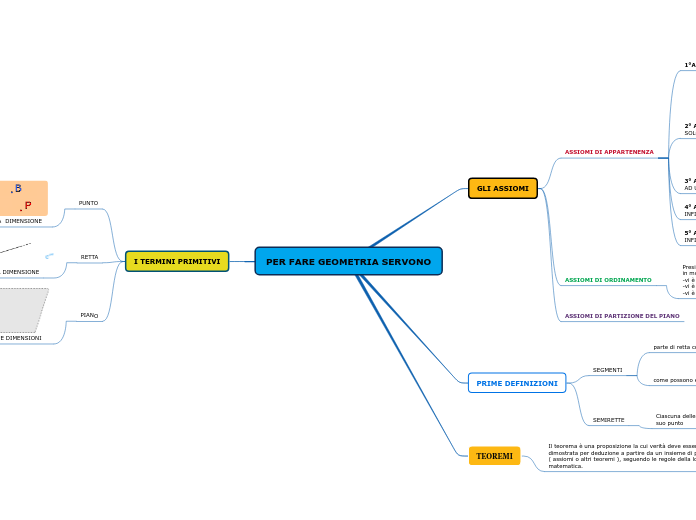
PER FARE GEOMETRIA SERVONO
GLI ASSIOMI
ASSIOMI DI APPARTENENZA
1°ASSIOMA: PER DUE PUNTI PASSA UNA SOLA RETTA

2° ASSIOMA: PER TRE PUNTI NON ALLINEATI PASSA UN SOLO PIANO
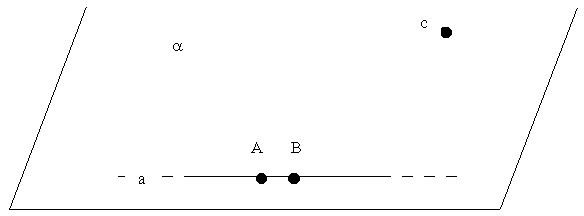
3° ASSIOMA: SE DUE PUNTI DI UNA RETTA APPARTENGONO AD UN PIANO , L'INTERA RETTA APPARTIENE AL PIANO
4° ASSIOMA: OGNI PIANO CONTIENE INFINITI PUNTI E INFINITE RETTE
5° ASSIOMA: LO SPAZIO CONTIENE INFINITI PUNTI INFINETE RETTE E INFINITI PIANI
ASSIOMI DI ORDINAMENTO
Presi due punti A e B distinti su una retta r orientata disegnati in modo tale che A precede B si ha che: --vi è almeno un punto che precede A
-vi è almeno un punto che segue A e precede B -vi è almeno un punto che segue B
TEOREMI
La retta contiene infiniti punti ed illimitata
Per un punto P di un piano passano infinite rette che appartengono al piano
ASSIOMI DI PARTIZIONE DEL PIANO
PRIME DEFINIZIONI
SEGMENTI
parte di retta compresa tra due suoi punti
come possono essere i segmenti?
ADIACENTI
CONSECUTIVI
SEMIRETTE
Ciascuna delle due parti in cui rimane divisa una retta da un suo punto
TEOREMI
Il teorema è una proposizione la cui verità deve essere dimostrata per deduzione a partire da un insieme di premesse ( assiomi o altri teoremi ), seguendo le regole della logica matematica.
I TERMINI PRIMITIVI
PUNTO

NON HA DIMENSIONE
RETTA
HA UNA SOLA DIMENSIONE
PIANO

HA DUE DIMENSIONI