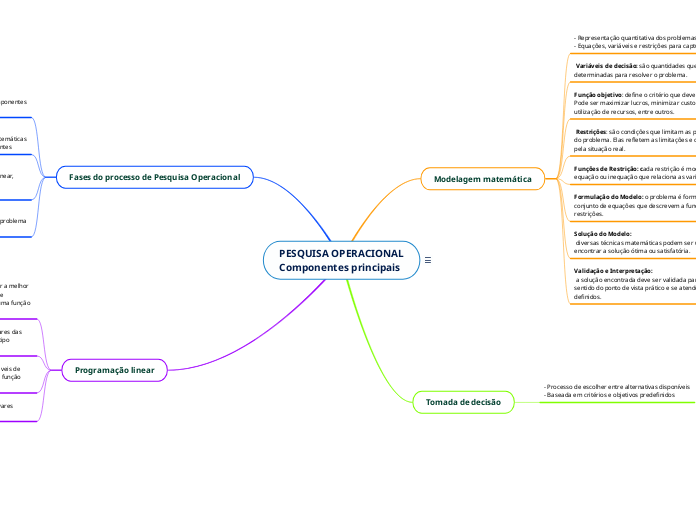
PESQUISA OPERACIONAL
Componentes principais
Modelagem matemática
- Representação quantitativa dos problemas do mundo real
- Equações, variáveis e restrições para capturar relações
Variáveis de decisão: são quantidades que precisam ser determinadas para resolver o problema.
Função objetivo: define o critério que deve ser otimizado. Pode ser maximizar lucros, minimizar custos, otimizar utilização de recursos, entre outros.
Restrições: são condições que limitam as possíveis soluções do problema. Elas refletem as limitações e condições impostas pela situação real.
Funções de Restrição: cada restrição é modelada por uma equação ou inequação que relaciona as variáveis de decisão.
Formulação do Modelo: o problema é formulado como um conjunto de equações que descrevem a função objetivo e as restrições.
Solução do Modelo:
diversas técnicas matemáticas podem ser usadas para encontrar a solução ótima ou satisfatória.
Validação e Interpretação:
a solução encontrada deve ser validada para verificar se faz sentido do ponto de vista prático e se atende aos objetivos definidos.
Tomada de decisão
- Processo de escolher entre alternativas disponíveis
- Baseada em critérios e objetivos predefinidos
Fases do processo de Pesquisa Operacional
Definição do Problema
- Identificação clara do problema e seus componentes
- Estabelecimento de objetivos e restrições
Construção do Modelo
- Transformação do problema em equações matemáticas
- Identificação de variáveis e parâmetros relevantes
Resolução do Modelo
- Utilização de técnicas matemáticas (programação linear, inteira, etc.)
- Encontrar solução ótima ou satisfatória
Validação e Implementação
- Verificação da solução em relação à realidade do problema
- Implementação da solução e monitoramento
Programação linear
Definição: técnica de otimização que visa encontrar a melhor solução para um problema, sujeito a um conjunto de restrições lineares, maximizando ou minimizando uma função linear chamada função objetivo.
Restrições: são expressas como combinações lineares das variáveis de decisão. As inequações podem ser do tipo
≤, ≥ ou = dependendo da natureza das restrições.
Solução Ótima: é um conjunto de valores das variáveis de decisão que satisfaz todas as restrições e otimiza a função objetivo.
Técnicas: Método Simplex, Análise Gráfica ou softwares especializados podem ser empregados.