Polynomials and Equations
Equation is a statement that say 2 expressions are equal. Ex: 3x+3=2x-1

Solution or root of an equation is the value of the variable that makes an equation true.
Simple Equations
To solve one step equation, do opposite operation to isolate the variable. Ex: x+4=13
x +4 -4 = 13 -4
x=9
To solve a 2 step equation, either add or subtract to isolate the variable term. Then divide by the coefficient of the variable term. Ex: 2x -7 = 9
2x -7 +7 = 9 +7
2x = 16
2x/2 = 16/2
x=8
Keep in mind that you are using SAMDEB
You can also do a check: L.S. = 2(8) - 7 R.S. = 9
=16 - 7
= 9
L.S. = R.S.

Multi-Step Equations
To solve an equation with Multiple Terms, collect variable terms one side and constant* terms on the other by doing opposite operation. Ex: 3x +2 = 2x -4
3x +2 -2x = 2x -4 -2x
x +2 = -4
x +2 -2 = -4 -2
x = -6

To solve equations with brackets, you need to expand them. 5 (y-3) - (y-2) = 19
5 (y-3) - (y-2) = 19
5y - 15 - y +2 = 19
4y - 13 = 19
4y - 13 + 13 = 19
4y = 32
4y/4 = 32/4
y=8
Check: L.S.= 5 (y-3) - (y-2) R.S.= 19
=5y - 15 - y +2
= 5 (8) - 15 - (8) + 2
=40 -15 -6
= 19
L.S.= R.S.
Equations with fractions
Eliminate the fraction by multiplying both side of the equation by the denominator.
6 = ⅓ (8+x)
3 ✕ 6 = 3 ✕ ⅓ (8+x)
18 = 8 + x
18 - 8 = 8 + x - 8
10 = x
For more than one fraction, find the LCD and multiply all the terms on both sides of equation by this value.
k + 2/3 = k - 4/ 5
15 ✕ k + 2/3 = 15 ✕k - 4/ 5
5 (k+2) = 3 (k-4)
5k + 10 = 3k - 12
5k + 10 - 3k - 10 = 3k - 12 - 3k - 10
2k = - 22
2k/2 = - 22/2
k = - 11

Modelling with Formulas
Algebraic relationship between two or more variables.
To rearrange, isolate the term that contains the variable, and then isolate the variable.
1 step: d = a + b
d - b = a + b - b
d - b = a
Or a = d - b
More then 1 step: y = mx + b
y - b = mx + b - b
y - b = mx
y - b/m = mx/m
y - b/m = x
Or x = y - b/m
Modelling with Algebra
It is a representation of a pattern of numbers.
Example: Alexa works at a record shop. She earns $!0.70/hr plus $0.88 for each album she sells. To model this situation we can say, "h " is the number of hours worked and "a" is the number of albums sold. The expression would be 10.70 h + 0.88 a
Expression VS Equation

Does not have an equal sign
Can't remove fraction (only expand)
We can only simplify

Has an equal sign
Fractions can be removed (by finding LCD)
We can solve
Polynomial
Made up of term(s) connected by addition or subtraction
operators.

To add, remove bracket, collect like terms: (2p-2)+(4p-7)
= 2p-2+4p-7
= 2p+4p-2-7
= 6p-9
To subtract, add its opposite: (3y+5)-(7y-4)
=(3y+5)+(-7y+4)
=3y+5-7y+4
=3y-7y+5+4
=-4y+9
Monomial
- 2a3b
Binomial
a3 - b3
Trinomial
x2 - 4x + 4
degree of a Polynomial
highest degree term
5x² - 7x = 2
Term

Like terms
identical variables with same exponents on each variable
Add: 4x+ 3x
= 7x
Subtract: 8x-3x
=5x
degree of a term
2/3xy= 1+1=2

Sum of exponents
4x²
Varriable= x²
Coefficient= 4
distributive property
Simplifies complicated expressions
Example:
Subtopic
Algebraic expression
Number, variables, operators
7x+3
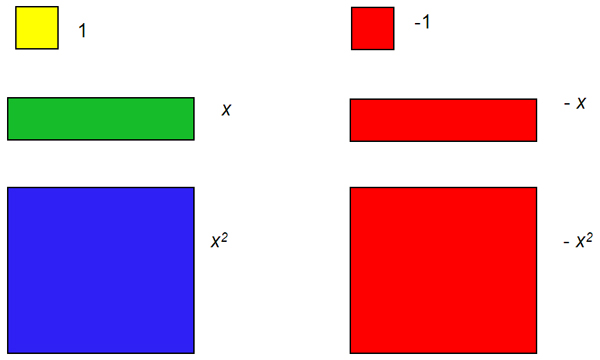
Modelling Tiles
Variable

w
Ex. 7×7×7=7³
Exponent= ³
base=7

Exponent Laws
Product Rule
Ex. xᵃ×xᵇ= xᵃ⁺ᵇ
Quotient Rule
Ex. xᵃ÷xᵇ= xᵃ⁻ᵇ
Power of Power Rule
Ex. (xᵃ)ᵇ= xᵃˣᵇ
