POTENCIAS, RAICES, LOGARITMOS Y NOTACIÓN CIENTÍFICO

POTENCIAS
BÁSICAS
1⁵=1
8⁰=1
3¹=3
BASES IGUALES
PRODUCTO
Se deja la misma base, pero se suman los exponentes: 2².2³=2⁵
DIVISIÓN
Se deja la misma base, pero se restan los exponentes. 5⁸/5³=5⁸¯³= 5⁵
POTENCIAS DE POTENCIAS
Se deja la misma base, pero el exponente se multiplica, por el exponente que se encuentra por fuera del paréntesis: (5³)²=5⁶
EXPONENTE IGUAL
Se deja el mismo exponente y se hace la operación indicada.4³.5³ = 20³
10⁴/2⁴= 5⁴
EXPONENTE ENTEROS -
Inverso de la multiplicación, de la base, elevada ;al exponente positivo: 8¯⁴= 1/8⁴
(8/5)¯⁵= 5⁵/8
EXPONENTE RACIONAL
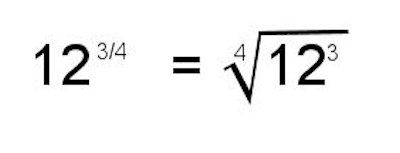
Topic principal
NOTACIÓN CIENTÍFICA
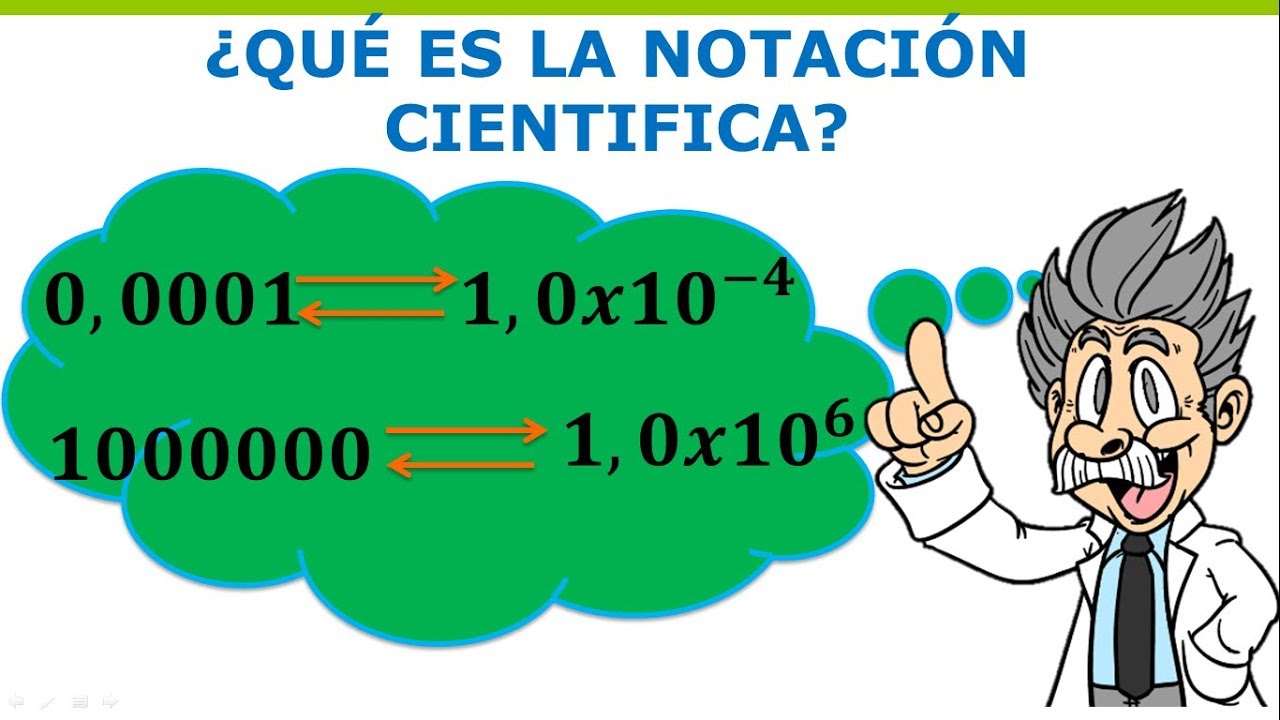
Sirve para expresar números de gran cantidad o de menor cantidad
CANTIDAD ENTERA
3.453.672= 3,453672x10⁶
35.400.000.000 = 3,5400000000x10¹⁰
CANTIDAD DECIMAL
1.783.672,01 = 1,78367201 x 10⁶
56.984.536,5 = 5,69845365 x 10⁷
CANTIDAD DECIMAL CON PARTE ENTERA CERO
0,0000005 = 5x 10¯⁷
0,0000000034 = 3,4 x 10¯⁹
EXPONENTE NEGATIVO
8,51x 10¯⁶=0,00000851
5,27 x10¯⁸= 0,0000000527
EXPONENTE POSITIVO
7,801x10⁸= 7,80100000
5,007x10¹⁰=5,0070000000
OPERACIONES
ADICCIÓN Y SUSTRACCIÓN
NÚMEROS CON IGUAL POTENCIA DE 10
4.89x10¹¹+ 3,02x10¹¹= (4,89+3,02) x10¹¹= 7,91x10¹¹
NÚMEROS CON DIFERENTES POTENCIA DE 10
8,24x10⁸+5,6x10⁶=8,24x10⁸+5,6x10⁶=(5,6x10¯²)x 10⁸+8,24x10⁸= 0,056x10⁸+8,24x10⁸ =8,296x10⁸
POTENCIACIÓN
( 7,5x10⁷)²= 7,5²x10¹⁴= 56.25x10¹⁴= 5.625x10¹⁵

RAICES

RACIONALIZACIÓN

EJEMPLOS




NUMEROS INAGINARIOS Y COMPLEJOS

Un número imaginario es un número complejo cuya parte real es igual a cero
REPRESENTACIÓN
CARTESIANA

Los números complejos se representan en unos ejes cartesianos. El eje X se llama eje real. El eje Y se llama eje imaginario
POLAR

La forma polar de un número complejo es otra forma de representar un número complejo
BINOMIAL
LOGARITMOS

Exponente al que hay que elevar un número, llamado base, para obtener otro número determinado
PROPIEDADES
1.El logaritmo de un producto es igual a la suma de los logaritmos de los factores:

2.El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor:

3.El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base:

4.El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz:

5.Cambio de base

MULTIPLICACIÓN Y DIVISIÓN
MULTIPLICACIÓN
7,83x10²⁰.5,2x10¯¹¹= (7,83x10²⁰) (5.2x10¯¹¹)= (7,83.5,2) (10²⁰x10¯¹¹)= 40,716x10²⁰¯¹¹= 40,716x10⁹ = 4,0716x10¹⁰
DIVISIÓN
5,25x10¹⁸/5x10¹⁰= 1,05x10¹⁸¯¹⁰= 1,05x10⁸
OPERACIONES

DIVISIÓN

RESTA

SUMA

La forma binómica de un número complejo es la expresión a+bi, a se llama la parte real y b la parte imaginaria.